|
|
Bien que disponible gratuitement pour que tout le monde y ait accès sans barrière, ce document n'est pas pour autant sans valeur. Vous pouvez participer aux frais de création et de diffusion, en vous rendant à la page contact.
Quiconque a un tant soit peu travaillé sur une maison 'traditionnelle' sait combien cela représente d'efforts. Avant même de commencer le chantier, ce sont des tonnes et des tonnes de matériaux qu'il faut charrier, que ce soit des pierres, du béton, des briques, des tuiles, des plaques de plâtres, des poutres ou des panneaux de bois. En plus cela coûte cher à transporter, à stocker, ainsi qu'à démolir et à s'en débarrasser une fois la maison parvenue à la fin de sa vie. D'où une aspiration légitime à des constructions plus légères, qui est aussi désir de ne plus se sentir enfermé dans ces tonnes de matières afin de renouer un contact plus intime avec les éléments.
Quiconque a passé au moins une nuit dans une tente de camping ou de randonnée sait que c'est possible. Sauf qu'après s'être battu pour la monter, s'être débattu pour la maintenir debout contre des éléments plus ou moins furieux, avoir subi l'inconfort de l'humidité et des flaques de boue, l'on n'est guère enclin à faire confiance à de telles structures légères en guise d'habitations permanentes, même dilatées à des dimensions plus confortables.
Quelques autoconstructeurs particulièrement motivés parviennent tout de même à concilier leur aspiration à la légèreté avec la solidité requise pour une habitation. Ils se tournent généralement vers des solutions éprouvées telles que tipis ou yourtes, voire pour les plus aventureux d'entre eux vers les dômes géodésiques. Tout ceci n'est pas forcément très séduisant, ni toujours très confortable dans notre contexte climatique tempéré, 'tempéré' signifiant qu'on subit un vaste échantillon d'extrêmes: chaud, froid, humidité, pluie, grêle, neige, vent et autres joyeusetés.
Ce genre de déconvenues n'incite pas à persévérer. Erreur! Presque tout le monde l'ignore, et cela vaut aussi pour les architectes et les autoconstructeurs, les structures légères ne se réduisent pas aux tentes ni aux huttes traditionnelles ni à des cabanes branlantes. De nombreuses réalisations remarquables (aérogares, salles de sports, halls d'expositions, etc., nous en verrons quelques unes dans les chapitres suivants) mettant en œuvre des procédés de construction légers s'offrent de plus en plus à notre regard. Ils n'ont plus grand chose à voir avec les tentes ou les huttes: coques en treillis, dômes géodésiques, structures tendues, structures pneumatiques, etc. Ils prouvent sans conteste qu'il est possible de faire léger, solide, confortable, élégant, y compris à de vastes échelles. D'ailleurs certains bâtiments de très grandes dimensions ne pourraient être réalisés autrement.
Hélas il n'y a guère de tentatives de transposer ces procédés à l'échelle de nos habitations. L'ignorance fait que, à choisir, l'on en revient toujours à ce que l'on connaît, à savoir empiler des matériaux solides, c'est-à-dire lourds. Pratiquement n'importe qui est capable de faire un bâtiment qui tient en empilant des pierres et en assemblant des poutres. A contrario très rares sont ceux qui parviennent à des résultats satisfaisants avec des matériaux légers tels que câbles et membranes. Tendre un simple vélum peut vite se transformer en cauchemar: à la moindre pluie des poches d'eau se forment, au moindre coup de vent la toile se met à battre pour finir par se déchirer. Il est possible d'éviter ces déconvenues mais il faut pour cela rentrer dans une toute autre logique structurale et constructive. Mis à part peut-être les marins, peu d'entre nous avons des intuitions valables concernant le comportement des matériaux souples.
Voilà pourquoi dans ce livre qui prétend faire le tour des structures légères, nous ne pouvons faire l'économie d'une descente au cœur de la matière. Si nous voulons construire des habitations légères qui soient aussi résistantes, confortables, élégantes, bon marchés, il nous faut commencer par comprendre quelles contraintes subit un bâtiment et comment la matière qui le constitue y réagit. Il s'agit de parvenir à sentir les forces qui l'animent pour devenir capables de jouer avec sans être contraints par elles, avec la même dextérité qu'un peintre joue sur sa toile avec les formes. Ou comme la Nature qui, soumise également aux contraintes physiques, parvient à déployer un nombre incalculable de formes. Donc comprendre la matière et les forces pour mieux se libérer de ces contraintes et ainsi être à même de déployer à notre tour toutes sortes de formes à la mesure de nos désirs-aspirations-besoins avec des principes structurels d'un naturel, d'une évidence et d'une simplicité qui sont gages de beauté et d'efficacité.
Rassurez-vous, cette première partie consacrée à la matière et aux forces ne va pas se transformer en un savant traité pour ingénieurs. Ne vous effrayez pas non plus si vous croisez une petite formule mathématique au détour d'une page. Ne fuyez surtout pas si vous y êtes allergiques, contentez-vous de passez outre. Hormis quelques rares passages, j'ai conçu ce livre pour être accessible au plus grand nombre sans connaissances préalables en architecture ou en physique.
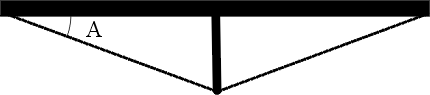
Commençons par un exemple concret, une structure simple et bien connue de tous que nul n'aura de difficulté à appréhender, l'arc. Je veux parler bien sûr de cette structure généralement en maçonnerie qui sert à faire des voûtes, des porches, des ponts, bref à relier deux points de la terre en passant par le ciel. Mais avant de parler architecture, je vous propose un petit exercice pour mieux ressentir les forces en présence.
Debout, jambes écartées, faites bien reposer votre poids sur vos deux pieds. Essayez de détendre au maximum les muscles de vos jambes pour mieux ressentir comment le poids de votre corps, centrer approximativement à hauteur du nombril, est canalisé vers le sol à travers les os des jambes. Faites osciller très légèrement votre bassins pour bien éprouver les sensations. Répétez l'exercice sur un sol glissant pour voir ce qui se passe. Attention...
Maintenant, en évitant de faire appel à vos souvenirs ni de regarder les figures des pages suivantes, dessinez un arc simple, dans votre tête ou bien sur le papier selon vos dispositions. Supposez-le construit de pierres et essayez d'imaginer les forces qui agissent à l'intérieur de la structure.
Passons en revue quelques variantes les plus communes.
D'abord il y a les faux arcs réalisés par simples empilements, soit en encorbellement (comme les bories des bergers provençaux) soit à l'aide d'un énorme linteau taillé en forme d'arc:
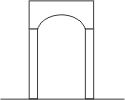
Certes ça tient mais ça pèse des tonnes et la portée est réduite, d'autant que l'épaisseur est la plus faible là où se concentrent les efforts, au milieu.
Plus abouti sur le plan structurel est l'arc en plein cintre, la grande spécialité des romains:
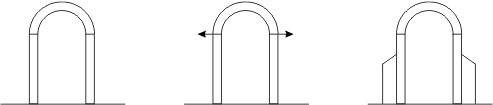
Un rapide coup d'œil sur la figure de gauche suggère que ça doit tenir. En fait pas toujours. La figure du milieu montre que la forme même de l'arc engendre des forces qui tendent à écarter les murs ou les colonnes sur lesquels il repose. Si l'appui n'est pas assez solide, tout s'effondre. La solution? Placer des contreforts, c'est-à-dire empiler des tonnes supplémentaires de pierres en saillie devant les murs pour les retenir (dessin de droite). Du coup l'élégance de la forme initiale en prend un sérieux coup, le moindre bâtiment prend l'allure d'une forteresse.
Même problème autre solution, l'arc brisé ou ogival:
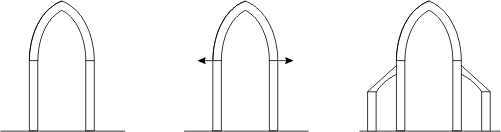
Encore plus élégant que le plein cintre et permettant de dégager plus d'espace, il bute néanmoins sur le même problème: des forces agissent qui tendent à écarter les colonnes. Toujours dans l'idée de dégager au maximum l'espace, la solution cette fois consiste à transférer la poussée plus loin à des culées via des arcs-boutants.
L'intérêt de ces exemples est de montrer que même si ces procédés ont donné naissance à des ouvrages remarquables que l'on admire encore de nos jours (comme le pont du Gard ou les cathédrales gothiques) ils ne témoignent pas d'une pleine compréhension des forces agissant sur la matière.
Il est assez facile d'imaginer l'histoire de l'arc. Il est probable qu'on a commencé par observer dans la Nature des petits arcs de pierres formés dans les torrents au gré des orages. On a dû ensuite s'efforcer de les reproduire. Comme c'était solide et que ça tenait bon, on a tenté de transposer le procédé à plus grande échelle. Hélas cette fois ça ne tenait plus. Alors on a bricolé des solutions, ajoutant du poids ici et là pour contrebuter les poussées d'écartement.
Pareille façon de procéder par essais et erreurs n'a évidemment rien de répréhensible: on apprend en faisant. La Nature elle-même ne procède pas autrement: les racines des arbres se renforcent d'elles-mêmes sous l'action de contraintes répétées, de même que nos muscles se développent en les exerçant, de sorte qu'ils peuvent travailler mieux en se fatiguant moins.
Le problème dans le cas de l'arc est que ce genre de bricolage peut conduire à contrevenir à l'intention initiale. Par exemple les cathédrales gothiques se voulaient de vastes espaces ouverts. Elles y parviennent dans la mesure où l'on évite de regarder à l'extérieur où toute l'énorme ossature qui fait tenir l'édifice est déportée. D'ailleurs à l'époque elle n'était guère visible, la cathédrale étant enserrée de toutes parts par d'innombrables habitations. Depuis que les espaces tout autour ont été dégagés, force est de reconnaître que les maîtres d'œuvre étaient de remarquables illusionnistes. Ceci dit sans méchanceté ni diminuer en rien leurs accomplissements. Ils ont fait de leur mieux avec les moyens techniques de l'époque, leur compréhension de la matière et des forces, et ce 'mieux' était vraiment merveilleux. On ne saurait leur reprocher de ne pas avoir tout compris. Surtout quand on voit combien de bâtisseurs contemporains, dont quelques uns portés aux nues, semblent n'avoir rien compris du tout, ignorant l'essentiel de la matière qu'ils sont censés manipuler et des hommes pour qui ils sont censés construire.
Certes l'illusionnisme est excusable dans certains cas mais j'estime qu'il vaut mieux l'éviter si l'on peut car cela projette un message ambigu. Dans le cas des cathédrales par exemple se mêlent sensations de lourdeur et de légèreté, sensations d'ouverture et de fermeture. Ambiguïté du même ordre que dans une communication entre humains lorsque les mots sortant de la bouche et le reste du corps expriment des choses contraires: malaise plus ou moins diffus chez l'interlocuteur.
Question: est-il possible de concevoir ce qui serait en quelque sorte la quintessence de l'arc en maçonnerie, une structure fine et élégante parce que optimale, permettant de franchir de vastes espaces tout en étant réellement légère et résistante?
Avant d'explorer cette question, reprenez le dessin d'un arc que vous avez fait tout à l'heure. À quoi ressemblait-il? À un arc traditionnel en plein cintre ou ogival? Dans ce cas, avez-vous bien senti les forces d'écartement qui tendent à faire s'écrouler la structure? Votre arc ressemblait-il à autre chose? Dans ce cas pensez-vous qu'il soit stable, capable de tenir par lui-même? Pouvez-vous commencer à imaginer une forme d'arc où les forces de gravité (on ne retiendra que celles-ci pour le moment) seraient parfaitement canalisées le long de l'arc lui-même, n'engendrant de ce fait aucun contrainte superflue et indésirable?
Ainsi posé le problème n'est pas évident. Mais, disons-le tout de suite, il a une solution. Pour la trouver, il est plus facile en fait de retourner le problème.
Question: quelle forme prend une corde, un câble ou une chaîne de masse linéique constante accrochée par deux points et pendant librement dans le champ de pesanteur?
Cette courbe est connue depuis des temps immémoriaux, depuis que les hommes utilisent des lianes, des cordes, des fils, etc. Son étude mathématique est évidemment beaucoup plus récente. Galilée pensait qu'il s'agissait d'un arc de parabole. Erreur! Leibniz, Bernoulli et Huygens ont montré indépendamment vers 1690 qu'il s'agit précisément d'un arc de cosinus hyperbolique. Pour les amateurs, une telle courbe a pour équation:
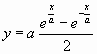
où a est un paramètre qui est fonction de la longueur de la corde, de sa masse linéique et de l'écartement entre les deux points d'accrochage.
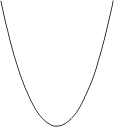
Chacun peut aisément voir à quoi ressemble cette courbe en laissant pendre un bout de cordelette ou une chaînette de médaillon (sans le médaillon évidemment), ou bien en regardant la forme que prend un câble électrique ou téléphonique entre deux pylônes. Pour cette raison elle est appelée chaînette ou courbe caténaire (du latin catena, chaîne) ou encore courbe funiculaire (du latin funiculus, corde) et plus rarement courbe vélaire car c'est aussi le profil que prend une voile rectangulaire attachée à deux barres horizontales enflée par un vent soufflant perpendiculairement à ces barres.
Remarque: le câble d'un pont suspendu prend quant à lui la forme d'un arc de parabole, si l'on considère la masse du câble négligeable par rapport à celle du tablier.
Prenons une chaîne et suspendons-la par ses deux extrémités. Comme nous venons de le voir elle pend en forme de chaînette. Maintenant soudons les maillons entre eux et renversons le profil ainsi rigidifié. Autre possibilité: prenons un fil, humidifions-le, suspendons-le dans le congélateur, et attendons quelques minutes qu'il gèle avant de le retirer et de le renverser. Dans les deux cas on obtient un arc idéal qui canalisent parfaitement le poids vers le sol.
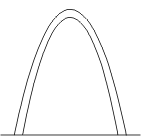
La raison est assez facile à comprendre. Lorsque la chaîne ou le fil pend librement, toutes les forces qui s'exercent à l'intérieur sont de pure traction. Lorsqu'on procède à son renversement, les forces de traction deviennent des forces de pure compression. On obtient ainsi un arc dans lequel les contraintes sont entièrement canalisées le long de l'arc lui-même. Il n'y a donc pas de poussées obliques, ce qui permet de faire l'économie de contreforts et autres arcs-boutants. Exemple: l'impressionnante Gateway Arch à Saint Louis aux Etats-Unis avec ses quelque 200 m de portée et autant en hauteur.

Bien qu'entièrement faite de béton, la Gateway Arch donne une réelle sensation de légèreté, sans les ambiguïtés qu'introduisent les contreforts et autres arcs-boutants.
Est-il possible d'aller vers encore plus de légèreté? Oui, à condition de passer à d'autres matériaux et d'autres procédés.
Considérez un pneu. Ramené à l'essentiel, c'est une membrane étanche en forme de tore remplie d'air sous pression, de l'ordre de 2 kg/cm². Quatre pneus supportent le poids d'une voiture, disons une tonne pour fixer les idées.
Une moitié de pneu, c'est une petite arche. On peut donc imaginer de véritables voûtes constituées de boudins gonflables:
 |
Ce genre d'objets commence à proliférer dans toutes sortes de manifestations sportives, promotionnelles et autres. On fait même des tentes de premiers secours qui ont l'avantage de se déployer toutes seules au moyen d'un petit compresseur.
On peut considérer qu'on atteint là le summum de la légèreté en matière d'arcs. On a tout de même du mal à imaginer une arche gonflable de 200 m de haut et de portée aussi fine que la Gateway Arch. Où est le problème?
Prenez une bouée d'enfant et gonflez-la bien. Demandez à quelqu'un de la maintenir verticale pendant que vous allez essayer de vous asseoir dessus. Boum patatras! ça ne tient pas! Pourquoi un pneu peut-il supporter le poids d'une voiture et une bouée de taille similaire ne supporte-t-elle pas le poids d'un homme? D'une part il y a l'absence de jante, d'autre part une énorme différence de pression, quelques grammes par centimètres carré dans la bouée contre plusieurs kilos dans un pneu. Si vous gonfliez la bouée à la même pression que le pneu, elle éclaterait. Autrement dit, une arche gonflable est d'autant plus apte à supporter du poids que la pression à l'intérieur est forte; mais plus ladite pression est importante, plus la membrane doit être solide sinon elle éclate.
Je reviendrai plus loin sur les structures gonflables. Je tenais toutefois à en parler dès à présent pour évoquer leur existence et leurs possibilités, ainsi que pour suggérer qu'on rentre dans une logique structurale résolument différente de ce à quoi l'on est habitué avec les empilages et les assemblages.
Un bâtiment est une forme matérielle, par opposition à une simple image (sur le papier, sur un écran, dans une tête), ou à un phénomène purement énergétique (barrière de force de type électromagnétique, acoustique ou autre, l'humanité n'est pas encore prête). En tant que forme, elle délimite un volume habitable. En tant qu'objet matériel, elle possède nécessairement une structure lui permettant de supporter des forces perturbatrices plus ou moins intenses: vent, neige, tremblements de terre, etc. L'exemple d'un objet architectural aussi basique que l'arc va nous servir de prétexte pour étudier quelques facettes des rapports entre forme et structure. En particulier le problème de la matérialisation de la forme et celui de la possible identité ou différence entre la forme et la structure.
Comparons la construction d'une arche en pierres semi-circulaire avec celle d'une arche funiculaire.
Dans le premier cas, la forme est très facile à décrire. Les outils de la géométrie euclidienne conviennent parfaitement. Il suffit de se donner un centre, le rayon du bord intérieur de l'arc, et celui du bord extérieur. Ces trois informations sont tout ce dont l'artisan a besoin pour réaliser l'arche. Avec une corde et un clou il est facile de tracer la forme au sol et délimiter chacun des claveaux (ou voussoirs), qui peuvent même être identiques si l'on veut. Le tailleur de pierres n'a plus qu'à se servir de ce patron pour débiter ses pierres pendant que le charpentier réalise le support semi-circulaire qui permettra leur pose.
Réaliser une arche funiculaire est une toute autre affaire car cette forme n'est pas un objet géométrique simple. On peut la définir analytiquement en résolvant une série d'équations en se donnant la hauteur, la portée et les contraintes. Leur complexité les rend impraticable sur le terrain: impossible de les transformer en une figure géométrique par un moyen simple. Force est de se contenter de calculer un certain nombre de points de la courbe à partir desquels sont délimités les claveaux, en interpolant la courbe entre les points.
On comprend que les romains, grands constructeurs d'arches en séries, se soient contentés de formes semi-circulaires et n'aient pas cherché une plus grande efficacité structurelle. La facilité de construction l'emportait sur le parfait contrôle des poussées, le problème d'avoir à contrebuter les arches et les voûtes en plein cintre étant facile à résoudre en empilant simplement des pierres.
Revenons à l'arche funiculaire. Il y a tout de même un moyen pratique de construire une telle arche qui ne nécessite aucun calcul ni aucun développement géométrique. C'est une méthode purement empirique qui passe par le retournement du problème comme on l'a vu avec la chaînette. Cela consiste à laisser pendre une chaîne, ou plusieurs entrecroisées dans le cas d'une surface plus complexe, et d'y suspendre à intervalles réguliers des poids proportionnels aux contraintes. On procède à des ajustements successifs de la longueur et des poids jusqu'à obtenir un résultat satisfaisant. Il n'y a plus qu'à dupliquer la forme et la remettre à l'échelle pour avoir un patron utilisable. C'est ainsi que procédait Antonio Gaudi sur la plupart de ses chantiers. Malgré leur allure déséquilibrée (on est tellement habitué à la rigoureuse verticalité que tout ce qui s'en éloigne sème le trouble!) ses bâtiments sont parfaitement conçus pour canaliser les forces au sol sans engendrer de poussées latérales. Le seul problème est que comme lui seul savait ce qu'il voulait et qu'il ne pouvait y avoir de plans, le travail s'arrêtait dès qu'il s'absentait. Sa fameuse église de la Colonia Guell près de Barcelone n'a jamais pu être terminée.
Ce problème du passage de la forme imaginée à la forme matérialisée débouche sur une autre question: est-il possible de réaliser des formes libres qui tiennent bon même si l'on est un simple architecte, voire un autoconstructeur, et pas un génie inspiré comme Antonio Gaudi ou Frei Otto, ni un grand cabinet d'architecture ayant à son service une armée d'ingénieurs équipés d'une batterie d'ordinateurs surpuissants? Autrement dit, est-il possible de sortir de la ligne droite et du cercle pour déployer relativement facilement des formes architecturales beaucoup plus organiques et attractives, mais tout aussi solides, voire plus pourquoi pas?
Observons que dans le monde vivant aucune forme n'est constituée de droites véritables ni de cercles, aucune forme n'est même descriptible dans le langage de la géométrie euclidienne. Pourtant la Nature les déploie en une variété incroyable, qui résistent fort bien à toutes sortes de contraintes. Il est donc clair que le problème soulevé tient aux limites de nos conceptions structurelles et pas aux limites de la matière. Si nous voulons libérer les formes architecturales, il nous faut commencer par libérer notre esprit de nos conceptions étriquées en matière de structures. Ce n'est qu'ainsi que l'on pourra inventer de nouveaux procédés structuraux. Mais il faudra prendre garde alors à ce que la forme ne devienne pas un simple sous-produit de la structure, au risque de retomber dans une facilité stérile et une désolante uniformité. Je m'explique:
L'arche funiculaire est apparue comme un optimum du point de vue structural. En fait sa forme est entièrement définie par les contraintes et ce qu'on appelle les conditions aux limites (les points d'accrochage de la corde et sa longueur). Qu'en est-il si la forme ainsi définie ne plait pas (on peut ne pas apprécier la sensation de convergence des montants) ou ne convient pas (on peut avoir besoin de murs verticaux et non obliques)? On en revient à des solutions moins parfaites du point de vue structurel telles que l'arche en plein cintre avec son lot de contreforts, ou bien l'arc ogival complété de ses arcs-boutants.
Autre manière de formuler le problème: tout en gardant la plus grande liberté de création s'agissant de la forme, est-il possible d'aller jusqu'à la confondre avec la structure ou bien faut-il les disjoindre? L'arche funiculaire est un exemple où forme et structure se confondent entièrement, tandis que dans les deux autres types d'arches les contreforts et les arcs-boutants font partie de la structure mais pas de la forme. Un exemple plus explicite va éclairer ce dilemme.
Voici deux formes architecturales libres (c'est-à-dire complètement libérées de la droite et du cercle) et très complexes:
 |
 |
La première est maintenant bien connue, il s'agit du musée Guggenheim de Bilbao conçu par Frank Gehry. C'est une forme que l'on peut qualifier de sculpturale. On a l'impression que ça ne va pas tenir, que certaines parties vont carrément se décrocher et tomber dans l'eau. Mais ça tient! Comment? quel rapport entre la sculpture et la structure? En fait les deux sont ici largement dissociés. Le bâtiment tient grâce à un complexe enchevêtrement de poutres d'acier qui constituent une solide ossature intérieure. La forme est en quelque sorte suspendue à cette ossature qui est en partie dissimulée dans les aménagements intérieurs.
Bien que plus ancien (1975) et tout aussi spectaculaire (plus de 7000 m² couverts) le second exemple est très peu connu. Il s'agit d'un énorme hall d'expositions situé à Mannheim et conçu par Frei Otto. Il est construit selon le procédé de la coque en treillis de bois dont le principe est détaillé dans la deuxième partie de ce livre. Retenons seulement pour l'instant cette caractéristique qui le différencie nettement de l'exemple précédent: il n'y a aucune ossature à l'intérieur. Le bâtiment est conçu de telle manière que forme et structure se confondent. Autrement dit, il est résistant par sa forme même. Cet accord entre la forme et la structure signifie que les forces sont parfaitement maîtrisées.
Pour autant on ne saurait réduire cette forme aux contraintes. Elle est en effet si complexe et si unique qu'elle est d'abord une création humaine avant d'être une réponse à des contraintes physiques. En fait la forme finale est le résultat d'un processus itératif: l'on part d'une première esquisse de la forme désirée; on voit comment elle se déforme sous l'action de contraintes; on apporte des correctifs pour se rapprocher à nouveau de la forme désirée; et ainsi de suite jusqu'à ce qu'un compromis satisfaisant soit trouvé. À ce point, forme et structure coïncident.
Ce genre de bâtiment qui tient sa résistance de sa forme peut être considéré comme un idéal. Il y a une économie de matière et de moyens qui est en cohérence avec la quête de légèreté que nous avons entreprise. Il y a aussi de l'honnêteté dans la mesure où rien n'est caché, tout est apparent, pas d'illusionnisme donc, pas de confusion des sensations.
Il devient de plus en plus évident que l'on a tendance à faire usage d'un vocabulaire structurel extrêmement limité, réservant la créativité presque exclusivement au domaine de la décoration. Cette pauvreté a pour contrecoup une très grande minceur du catalogue de formes disponibles, avec prédominance de la ligne droite et du cercle.
L'on a trop tendance également à réserver les innovations dans ce domaine à des projets de prestige et se contenter de solutions banales pour nos maisons et autres bâtiments de notre environnement quotidien. Dire qu'on utilise tel ou tel procédé depuis des lustres et qu'il marche n'est pas une raison valable. D'abord ça ne marche pas toujours aussi bien qu'on le voudrait: quand on y regarde de près, c'est incroyable le nombre de maisons dites traditionnelles qui présentent des fissures et autres problèmes structuraux.
Dire que l'innovation coûte chère n'est pas non plus une raison valable. C'est méconnaître que les structures légères sont presque toujours moins coûteuses que leurs équivalents en dur.
Enfin, des formes nouvelles appellent nécessairement des solutions structurales nouvelles. Il ne viendrait l'idée à personne de construire un dôme en parpaings. J'ajoute que faire du béton avec du chanvre ou remplacer les briques par des ballots de paille n'est pas faire preuve d'imagination en matière de structures dans la mesure où cela reste dans une logique éculée d'empilement.
Pour se remettre à inventer, il faut procéder à un renversement: ne plus considérer la matière et les forces comme des contraintes qui limitent notre expression mais comme une occasion de jouer avec pour créer. Nous pouvons rêver sans contraintes à des formes qui correspondent à ce que nous sommes, ce que nous désirons vivre, ce que nous souhaitons devenir. Il se peut que certaines de ces formes rêvées s'avèrent irréalisables: ce n'est pas grave, c'est juste que le sens qu'elles portent pour l'homme n'est pas encore approprié à son degré d'évolution. Le jour où le collectif sera prêt, c'est-à-dire où la conscience sera suffisamment ouverte pour accéder à de nouveaux territoires de sensations et de significations, alors des procédés seront trouvés qui permettront de les réaliser.
Le meilleur exemple qui me vient pour illustrer ce propos est celui du vol aérien. Beaucoup en ont rêvé par le passé mais tous se sont trompés sur le moyen d'y arriver: imiter les oiseaux qui battent des ailes. C'est impossible car il y a un problème de transgression d'échelle: ce qui marche pour un insecte ou un oiseau ne marche pas à la dimension d'un être humain. Finalement on a réussi à voler en mettant en œuvre des procédés radicalement différents. D'abord avec le principe du plus léger que l'air (ballons à air chaud suivis des ballons à hydrogène et à hélium), puis en mettant à profit le phénomène de portance, c'est-à-dire qu'une aile qui avance dans l'air est littéralement soulevée par la dépression créée sur sa surface supérieure convexe (principe de l'avion mais aussi du deltaplane et du parapente).
Il est important de remarquer que la montgolfière ou le parapente auraient pu être réalisés des siècles plus tôt étant donné qu'ils ne réclament que des capacités techniques minimes (on peut facilement faire un parapente en sachant seulement filer et tisser la soie). D'autant qu'on savait faire depuis longtemps des voiles et des cerfs-volants tant qu'en Orient qu'en Occident. Donc pareille invention, avant d'être une affaire de technique, était bel et bien un problème de conscience. Je crois qu'avant la fin du 18e siècle, l'humanité n'était pas prête à s'envoler. Je rappelle que c'est le siècle des lumières, époque où les idées de conquête de la Nature, de progrès, de dépassement du géocentrisme imprègnent une grande partie de la population de l'Europe et plus seulement une élite (voir l'ouvrage du même auteur les grandes civilisations).
Voilà un exemple de l'imagination à l'œuvre pour concrétiser un rêve. Il est grand temps de mettre cette faculté au service de l'architecture pour nous sortir enfin de ces pesantes boîtes parallélépipédiques, si laides à forces d'être répétées. Certes elles conviennent tout à fait à un homme craintif et coupé de la Nature mais plus à un homme qui s'est allégé et ouvert à l'univers. Il est donc grand temps d'inventer des structures et des formes architecturales qui, à l'échelle de nos habitations, incarnent nos nouveaux accomplissements, nos nouveaux rêves, et nous fassent rêver encore plus loin. Déjà retrouver un rapport plus intime, plus subtile, plus sensuel avec tout ce qui nous entoure, ce qui passe nécessairement par plus de légèreté.
Pour parvenir à jouer véritablement avec la matière, il en faut un minimum de compréhension. Sans que cela se transforme en un cours de physique, je propose une approche pratique à l'échelle humaine centrée sur les problèmes architecturaux. Nous allons partir du connu pour aller progressivement vers du moins connu, voire du pas connu du tout, mais tellement plus riche de perspectives.
Le but d'une structure architecturale est d'assurer l'intégrité d'une forme habitable malgré les forces qui agissent sur elle et qui tendent à la déstabiliser. Cela ne veut pas dire qu'elle doive être définitivement figée. Elle peut bouger ou se déformer de manière élastique. On peut même imaginer des structures adaptatives qui se modifieraient en fonction des contraintes, à l'instar de stores s'ouvrant et se fermant selon l'ensoleillement.
Quoiqu'il en soit, que la réaction du bâtiment à l'action de ces forces soit la rigidité, la déformabilité ou l'adaptabilité, le maintien de l'intégrité passe en général par la canalisation jusqu'au sol des forces auxquelles elle est soumise, à commencer par son propre poids. Je dis ˝en général˝ car nous verrons que les structures pneumatiques ou celles conçues selon les principes de la tenségrité fonctionnent différemment. Mais ce sera pour plus tard et pour le moment restons dans du connu. Tellement connu même que nous l'expérimentons continuellement sans guère y prêter attention. Si vous vous campez bien droit sur vos pieds, sans bouger, vous sentirez le poids de votre corps qui aboutit au sol, lequel d'ailleurs se creuse s'il est meuble, preuve que vous êtes bien attiré par la gravité vers le centre de la Terre et pas en suspension au-dessus du sol. La plupart des structures architecturales se comportent de la même manière. Vous pouvez imaginer ces forces comme analogues à un liquide courant dans une succession de tuyaux. Les colonnes, poutres, câbles, membranes et autres éléments structuraux sont ces tuyaux qui ont pour rôle de conduire les charges jusqu'au sol où elles se perdent...
Un des principaux défis des architectes en tous temps et tous lieux est de refermer un espace habitable au sein du plus vaste espace dans lequel nous déployons notre corps et nous mouvons. Comme nous sommes une espèce vivant sur Terre (et pas dans l'eau ni dans les airs ni dans l'espace interstellaire) tous les bâtiments sont avant tout conditionnés par la force de gravité. Elle influe directement sur la forme, puisque les êtres humains doivent pouvoir se mouvoir principalement dans le plan horizontal. Remarquons qu'un immeuble, même très haut comme un gratte-ciel, est essentiellement une superposition de plans horizontaux. Remarquons également la difficulté d'organiser l'espace pour la vie des hommes dans des formes qui ne se partitionnent pas aisément en plans horizontaux comme les tubes que sont les sous-marins ou les stations spatiales.
La gravité influe aussi directement sur la structure, puisque la perpendiculaire au plan horizontal est la direction verticale selon laquelle s'exerce la force de gravité, autrement dit le poids.
En fait la gravité, seule force généralement prise en compte dans les structures faites de matériaux empilés, n'est pas toujours la plus grande des forces qui s'exercent sur un bâtiment. Nous allons voir que les forces de succion du vent ou de cisaillement des tremblements de terre peuvent être bien plus considérables. En revanche j'exclus de mon propos:
- les vagues et autres courants d'eau qui ne s'appliquent qu'à des cas très particuliers tels que maisons sur pilotis, moulins à eau ou piles de ponts (mon sujet est principalement l'habitat, pas les ouvrages d'art);
- les effets de marée qui ne jouent, et encore de manière à peine décelable, que sur des bâtiments immenses, au moins plusieurs kilomètres (un seul même à ma connaissance, le grand anneau de collision du CERN près de Genève);
- les forces électromagnétiques, sans influence décelable sur les structures, même métalliques (ce qui ne veut pas dire qu'elles n'aient pas d'autres influences, mais c'est une autre histoire...);
- les dilatations-contractions dues à de très forts écarts de températures (non négligeables sur de grandes structures de métal et/ou de verre exposant une surface au soleil et l'autre à l'ombre);
- les vibrations.
Détaillons à présent les principales forces retenues:
1. l'attraction vers le bas de la gravité,
2. les poussées et aspirations dues au vent,
3. les tremblements de terre.
La force la mieux connue et souvent la seule prise en compte dans les habitations est la gravitation, ou plus prosaïquement poids. Direction et intensité sont faciles à évaluer:
- la direction est toujours verticale (c'est même la définition de la verticale);
- l'intensité se répartit entre charges fixes, correspondant au poids du bâtiment lui-même, et charges variables telles que surcharges neigeuses ou poids des occupants.
Quelques valeurs pour se faire une idée:
- un mètre carré d'un mur plein de 12 centimètres d'épaisseur (respectivement 24 cm) pèse environ 200 kg (resp. 400 kg) s'il est fait en pierres calcaires, 240 kg (resp. 480) en briques, et 275 kg (resp. 550) en béton plein;
- un madrier de 110x225 mm de section et 4 m de long en chêne pèse 75 kg, et 43 kg en pin;
- en plaine, compter une surcharge de neige de l'ordre de 50 kg/m², et 200 kg/m² à 1000 m d'altitude (il existe pour chaque pays des tables donnant les valeurs précises à prendre en compte en fonction de la région et de l'altitude);
- les charges que supporte un plancher d'habitation sont de l'ordre de 150 kg/m².
Voilà pour ce qui concerne l'action de la force gravitationnelle. Quant à la réaction de la structure, elle est plus complexe qu'on ne l'imagine.
Concernant la direction, un poids vertical peut facilement se transformer en une poussée latérale. On l'a bien vu dans le cas de l'arc, qui tend à s'écarter sous l'action de son propre poids (ou de diverses surcharges). Cette réaction indésirable doit être rattrapée, par exemple par des contreforts ou des arcs-boutants s'appuyant sur des culées, voire de simples tirants si l'effet n'est pas trop important.
Concernant l'intensité, elle aussi peut varier considérablement. Par exemple une structure en porte-à-faux peut amplifier des efforts par effet de levier. Prenez un gros dictionnaire, portez-le à bout de bras puis ramenez votre bras contre votre corps, vous sentirez comme le poids semble changer.
Autre exemple:
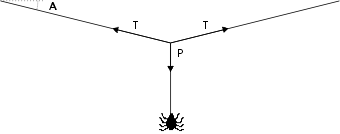
La tension dans le fil vaut précisément:
![]()
où P est le poids et A l'angle que fait le fil avec l'horizontale.
La présence de l'inverse d'un sinus est problématique car c'est une fonction qui croit très vite avec la fermeture de l'angle:
|
A |
30° |
15° |
10° |
5° |
|
1/sinA |
2 |
3,9 |
5,8 |
11,5 |
Cela signifie que pour un angle très fermé de 5°, la tension équivaut à presque 6 fois le poids!
L'apparente simplicité de l'action de la force gravitationnelle sur un bâtiment ne doit donc pas nous leurrer. Certes sa direction est toujours la même (verticale) et son intensité varie dans des limites bien connues (même les charges dites variables sont relativement faciles à évaluer). Mais la manière dont le bâtiment réagit au poids n'est pas aussi simple. On peut voir surgir des forces dans des directions inattendues et qui prennent des valeurs très élevées. C'est contraire à l'idée que l'on se fait intuitivement de la transmission de cette forces. On serait plutôt de croire que puisqu'elle est verticale les réactions de la structure doivent être elles aussi verticales et du même ordre de grandeur. C'est cette conception 'naïve' qui a probablement longtemps retardé l'invention d'une solution efficace au problème de l'arc.
L'essentiel à retenir est que la réaction globale d'une structure est très différente en direction et en intensité de l'action qu'elle subit. Ceci est encore accentué dans le cas de la deuxième grande force à prendre en compte, le vent.
Disons pour commencer que l'énergie du vent n'est rien d'autre que l'énergie cinétique de la masse d'air déplacée. Si vous recevez un ballon très fort, vous reculez sous le choc. Eh bien il en va de même sous l'effet d'une masse d'air qui se déplace à grande vitesse. Plus précisément, lorsque cette masse rencontre un obstacle, plusieurs choses peuvent se produire:
1. L'énergie est absorbée, ce qui se traduit par une augmentation de la pression à la surface de l'objet. Dans le cas où toute l'énergie est transformée en pression, l'augmentation de pression vaut:
![]()
où d est la masse volumique de l'air et V la vitesse (avec V est en m/s et D en kg/m3, P est exprimé en Pa).
C'est ce phénomène qui est exploité par les voiliers pour avancer, ou par les moulins à vent pour actionner leur meule (mais pas par les éoliennes modernes: voir point 3).
Pour fixer les idées et avec des unités plus parlantes:
|
V en km/h |
30 |
60 |
120 |
240 |
|
P en kg/m² |
4,6 |
18,5 |
73 |
290 |
2. En heurtant l'obstacle, l'air est dévié, ce qui donne lieu fréquemment à des turbulences imprévisibles. On le voit bien aux mouvements d'un drapeau, du linge sur un étendage, ou des tourbillons de la fumée qui sort d'une cheminée.
3. L'air peut même être accéléré, ce qui engendre alors une dépression. C'est ce phénomène qui explique la portance d'une aile d'avion ainsi que le fonctionnement de l'hélice. Contrairement à la conception naïve qui a longtemps prévalu au point de bloquer tout progrès en matière d'aviation, ce n'est pas une surpression sous l'aile qui assure la portance mais une dépression sur l'aile. Pour ajouter encore à la bizarrerie, cette dépression peut atteindre des valeurs de beaucoup supérieures à la surpression maximale donnée par la formule ci-dessus. Une expérience simple permet de vérifier l'existence de ce phénomène. Prenez une feuille de papier ordinaire, posez un bord sur la lèvre inférieure et soufflez droit devant. Si la position est correcte et si vous soufflez assez fort, vous devriez voir la feuille se soulever. C'est un effet de la dépression créée au-dessus par l'air qui s'écoule rapidement.
Concrètement, comment réagit un bâtiment au souffle du vent? Le schéma suivant résume les principaux effets:
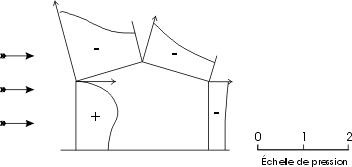
Les petits graphiques placés au niveau des murs et des toits indiquent l'intensité de la surpression (signe +) ou de la dépression (signe -) par rapport à la valeur calculée avec la formule ci-dessus et que l'on appelle pression de stagnation.
Lorsque le vent frappe perpendiculairement un mur vertical, il subit une surpression, à l'instar d'une voile de navire qui se gonfle. Au centre, la pression atteint pratiquement la pression de stagnation. En s'éloignant du centre, elle décroît, pour s'annuler sur les bords où le flux d'air, après avoir été dévié perpendiculairement à sa course, reprend sa trajectoire.
Derrière le mur, la pression est généralement inférieure à la pression ambiante. Il se produit une aspiration, comme derrière une automobile qui roule vite. Son intensité est de l'ordre de -0,5 à -0,7 fois la pression de stagnation. Le phénomène est facile à observer lorsqu'un feu brûle dans une cheminée: on voit souvent la fumée se rabattre contre le mur abrité du vent.
Au niveau de la toiture, les choses sont encore plus compliquées. En la supposant faite de surfaces planes et régulières comme sur le schéma, les facteurs principaux qui interviennent sont la hauteur du bâtiment et la pente de la toiture.
Il existe une inclinaison de la toiture appelée angle critique pour laquelle le coefficient d'aspiration atteint un maximum, entre -0,7 et -1,4, soit parfois une intensité supérieure à la pression de stagnation. Cet angle dépend surtout de la hauteur de l'édifice: environ 5° pour un bâtiment très bas, de 5 à 15° pour une villa de plain-pied, environ 30° pour un bâtiment plus élevé ayant un rapport hauteur/largeur jusqu'à 2, etc.
Pour un bâtiment donné, et donc un angle critique donné, plus la pente du toit s'accentue au-delà de l'angle critique, plus l'aspiration diminue. Le coefficient de pression s'annule même pour un angle compris entre 20 et 45° proportionnel à la hauteur du bâtiment. Au-delà, lorsque la pente augmente encore, le toit devenant de plus en plus vertical, on retrouve une situation de surpression.
Ceci vaut pour un flux d'air régulier et bien horizontal qui rencontre un bâtiment aux formes elles aussi régulières et bien orientées. En réalité le vent est plus souvent turbulent, avec des sautes subites d'intensité et de direction. Quant aux bâtiments, ils ont souvent des orientations qui leur font prendre le vent en oblique, des formes qui perturbent notablement l'écoulement de l'air (ce que l'on observe à l'augmentation ou à la baisse de tirage d'une cheminée selon la direction du vent), et des interactions avec l'environnement qui créent des couloirs d'accélération ou des tourbillons violents. Tout ceci peut aboutir localement à de très forts effets de succion. Un coefficient de -2 n'est pas rare, pouvant parfois atteindre -5. Cela signifie concrètement que pour un vent de 120 km/h on peut avoir en certains points des effets d'aspiration de 150 kg/m² voire jusqu'à 350 kg/m². C'est plus que le poids d'une couverture et orienté dans la direction opposée. Ne parlons pas des effets d'un ouragan avec des vents soufflant à 240 km/h (je rappelle que l'intensité de tous ces phénomènes augmente comme le carré de la vitesse). Nulle surprise donc si les toits s'envolent si facilement lors des tempêtes.
Le problème avec le vent c'est que les rafales sont imprévisibles et qu'elles peuvent avoir des effets plus intenses que la gravité. On comprend les dommages que subissent des bâtiments conçus en général pour résister uniquement au poids. Les grands bâtiments modernes, des gratte-ciel aux immenses halls, prennent évidemment en compte ce facteur. Ils sont testés en soufflerie pour étudier leurs réactions.
S'agissant de toutes petites structures comme des tentes de camping ou de randonnée, le phénomène est bien connu et relativement facile à maîtriser. Il suffit de les arrimer à l'aide de cordes et de piquets, ce qui n'empêche pas de temps en temps de voir une toile s'envoler.
Entre ces extrêmes règne une grande ignorance et seule l'expérience permet de s'en sortir sans trop de dommages. Ainsi ces lourdes pierres posées sur les toits de tuiles des maisons traditionnelles provençales où souffle souvent un fort Mistral. Parfois cela suffit, parfois non: cf. les récents ouragans dans les Caraïbes et le golfe du Mexique. En tout cas il est probable que cela ne suffira pas si l'on se lance dans des constructions aux formes nouvelles pour lesquelles on ne dispose d'aucun recul. Sans faire forcément des études aérodynamiques poussées ni des modélisations complexes, retenons au moins ceci:
1. les effets du vent augmentent avec la hauteur;
2. la forme du bâtiment joue un rôle majeur, selon qu'elle se présente comme un obstacle sur lequel le vent vient buter ou comme une simple présence qui dévie gentiment l'écoulement (comparer l'effet d'un dôme à celui d'un parallélépipède);
3. le mariage avec les formes environnantes (végétation, autres bâtiments, creux et bosses du terrain) peut, selon qu'il est réussi ou non, produire des effets d'écran mutuellement bénéfiques ou au contraire jouer le rôle d'amplificateur des perturbations.
Comparer à ce propos les rues et places traditionnelles des vieux villages provençaux qui restent fréquentables même par temps de Mistral avec les rues et places des extensions urbaines plus récentes, triomphe de la ligne droite.
Posez quelques livres dans le plat de votre main, 4 ou 5 livres de poche par exemple. Première expérience: effectuez un petit mouvement brusque vers le haut ou vers le bas. S'il est suffisamment proche de la verticale, l'empilage doit à peine dévier. Deuxième expérience: effectuez un brusque mouvement latéral. Cette fois l'empilage est détruit même si l'amplitude reste faible.
Ceci permet de comprendre que les effets les plus destructeurs des secousses sismiques ne sont pas les mouvements verticaux (soulèvement ou abaissement) mais les mouvements horizontaux (forces de cisaillement). Les bâtiments conçus pour résister principalement aux forces verticales de gravité réagissent très mal à ces forces de cisaillement: les empilages se fissures et s'écroulent tandis que les cadres rigides se déforment en losange et finissent par se disloquer voire se briser. Les structures plus légères et plus souples réagissent évidemment beaucoup mieux.
Les trois grandes forces que l'on vient d'étudier agissent sur la structure depuis l'extérieur. D'autres forces interviennent parfois qui sont internes à la structure même. Je ne vais pas insister car elles seront détaillées le moment venu dans les chapitres consacrés à la tenségrité et aux structures tendues. Un exemple tout de même pour se faire dès à présent une idée de leur ampleur:
Le Hoosier Dome d'Indianapolis est un immense stade capable d'accueillir plus de 60 000 personnes. Son toit est fait d'une membrane très fine (deux couches de 0,8 mm chacune) de tissu de verre enduit de téflon. Elle est gonflée par une très légère surpression de 2,45 g/cm², soit dix fois moins que les variations de pression atmosphérique. Ce n'est pas grand chose mais appliquée aux 32 400 m² de toit, cela fait une force de soulèvement de près de 800 tonnes. Comme aucune membrane n'y résisterait, celle-ci est en fait tenue par un réseau de câbles d'acier. L'ensemble du toit pèse 233 tonnes, à comparer avec les 800 tonnes de surpression.
Ce qu'il importe de retenir ici, c'est que la tension a une fonction structurale. Ce n'est pas une force extérieure qui déstabilise l'édifice, c'est au contraire une tension interne qui assure sa stabilité et lui confère sa résistance.
|
forces |
actions |
réactions |
||
|
intensité |
direction |
durée |
||
|
gravité |
proportionnelle à la masse |
vers le bas |
continue |
effet multiplicateur dû à la géométrie de la structure |
|
vent |
proportionnelle à la surface et au carré de la vitesse |
toutes |
continue et discontinue (rafales) |
surpression ou aspiration selon la forme de la surface |
|
séismes |
variable |
verticale et horizontale |
secousses brèves parfois répétées |
fonction de la rigidité de la structure et de la masse |
On voit que des caractéristiques très différentes du bâtiment interviennent en réaction à ces différentes forces: masse de l'édifice, étendue et forme de la surface, géométrie et rigidité de la structure. On peut jouer sur tous ces facteurs. Dans tous les cas une réduction de la masse et une certaine flexibilité de la structure semblent avantageuses. Quant à la forme, elle n'est critique que dans les zones de vents violents et doit être alors véritablement conçue comme un organisme aérien avec une intégration poussée dans l'environnement.
Que se passe-t-il au cœur même de la matière pour conférer à la structure d'un bâtiment sa résistance à ces efforts? Aussi complexe qu'il soit, aussi diverses que soient les forces qui s'exercent dessus, un élément de structure réagit essentiellement de deux manières: il s'étire sous l'effet de la tension ou s'écrase sous l'effet de la compression.
D'autres forces interviennent comme la flexion, la torsion ou le cisaillement. Ce ne sont en fait que des combinaisons de ces deux forces primordiales. S'agissant de la flexion, nous verrons plus loin. S'agissant de la torsion, il est facile de s'en rendre compte en prenant un bout de ficelle et en l'entortillant au maximum jusqu'à former une petite tige rigide: rien d'autre qu'une gaine en tension enserrant un cœur en compression. Quant au cisaillement, il correspond à un phénomène de glissement au sein de la matière qui lui aussi se résout au final en une combinaison de tension et de compression, quoique de manière plus complexe.
Tension et compression sont des forces complémentaires tant localement que globalement. Localement signifie que dans un élément de structure il est rare d'avoir uniquement de la tension ou uniquement de la compression. Il faudrait plutôt dire que la tension prédomine, ou que la compression prédomine. De même au niveau global, c'est-à-dire dans la totalité de la structure, les éléments où prédominent la tension doivent être contrebalancés par d'autres où prédomine la compression afin que l'ensemble soit en équilibre.
Alors que dans toute structure ces deux forces sont également importantes, les structures architecturales ont, jusqu'à une époque récente, largement ignoré la tension pour se concentrer quasi exclusivement sur la compression.
L'argument selon lequel cela viendrait d'une plus grande disponibilité de matériaux travaillant bien en compression que de matériaux travaillant bien en tension ne tient évidemment pas. Les deux se trouvent dans l'environnement avec une égale facilité, comme la pierre pour les premiers et les fibres végétales pour les seconds.
Ni celui selon lequel ce serait trop compliqué. Depuis des millénaires, dans toutes les contrées du monde, les hommes ne se sont pas privés de réaliser des structures tendues comme des voiliers ou des ponts suspendus (les chinois en faisaient avec des cordes de bambou dont la portée dépassait parfois les deux cents mètres). Ces ouvrages ne sont pas plus compliqués à réaliser que des voûtes en pierres. Mais curieusement le principe n'a pas été étendu aux maisons.
Problème de durabilité des matériaux peut-être: comparer les soins que réclame un voilier à ceux que réclame une maison en pierre. Ou problème de qualification de la main d'œuvre. Il est certain que construire des petits bâtiments en empilant simplement des matériaux ne réclame guère de compétences, que ce soient des branches, des rondins, des pierres, de la terre, ou autres. Les empilements ont un autre avantage: si ça ne tient pas bien, il n'y a pas besoin d'être plus qualifié pour renforcer la structure, il suffit d'en empiler encore et encore. De tels bâtiments résistent généralement bien à la force de gravité parce qu'elle reste constante en valeur et en direction (à condition que le terrain résiste lui aussi, ce qui n'est pas toujours le cas), et le poids comprime les matériaux empilés, choisis justement pour leur résistance à ce type d'effort. En revanche ils résistent très mal à toutes les autres forces. L'histoire tant lointaine que récente est pleine de catastrophes où des villes entières sont détruites par des tremblements de terre, des ouragans ou des inondations.
Pour couvrir l'espace, les hommes emploient un tout petit catalogue de structures de bases. Assemblées et combinées, elles aboutissent à une relative variété d'édifices. Qu'elle soit en bois, en pierre, en métal, en béton, etc., la poutre est sans conteste le procédé constructif le plus simple et le plus répandu pour enjamber un espace et le couvrir: un tronc jeté entre deux rives d'un torrent, c'est déjà un pont; quelques poutres placées en appui sur des rochers ou sur des poteaux et recouvertes de branches, c'est déjà un toit, presque une maison...
Poteaux et poutres se distinguent seulement par la direction principale des efforts qu'ils subissent: une poutre, généralement horizontale, est soumise principalement à des efforts transversaux, c'est-à-dire perpendiculaires à sa longueur, tandis qu'un poteau est placé verticalement et subit des efforts longitudinaux, c'est-à-dire selon son axe. Ceci dit pour simplifier car il y a évidemment tous les cas intermédiaires comme les arbalétriers d'une charpente plus ou moins inclinés. Remarquons aussi qu'un mât de voilier, bien que vertical, travaille plutôt comme une poutre que comme un poteau. Idem pour un arbre. Quoiqu'il en soit, poteaux et poutres réagissent de la même manière aux efforts qu'ils subissent en fléchissant, et cette flexion n'est rien d'autre qu'un jeu complémentaire de tensions et de compressions.
Prenez un gros livre à couverture souple ou un gros catalogue du genre vente par correspondance. Tenez fermement la reliure d'une main et de l'autre courbez l'ouvrage. Vous devez observer du côté où elles ne sont pas reliées un glissement des feuilles les unes par rapport aux autres, le bord libre qui était droit devenant oblique.
Maintenant imaginez une poutre soumise à une charge. Que la poutre soit en bois, en béton ou en acier ne change rien. Que la charge soit longitudinale ou transversale ne change rien non plus: la poutre va se courber sous l'effort.
Que se passe-t-il lorsqu'elle se courbe? Contrairement à un livre qui est constitué de pages indépendantes susceptibles de glisser les unes par rapport aux autres, une poutre est un ensemble monobloc. Elle ne peut donc absorber la déformation globale qu'en se déformant au cœur même de sa matière. En regardant comment le catalogue s'est courbé, vous devinerez sans peine comment la poutre va devoir se déformer pour se courber sans se briser: le côté intérieur concave se raccourcit en subissant une compression, tandis que le côté extérieur convexe s'étire sous l'effet d'une tension.
Que se passe-t-il au milieu de la poutre, entre la zone étirée et celle contractée? Il y a forcément une zone qui n'est ni étirée ni contractée où ne règne ni tension ni compression. En exagérant à peine on peut dire que la matière située à cet endroit ne sert à rien. Plus précisément, elle maintient ensemble les différentes parties de la poutre mais ne contribue aucunement à sa résistance. On peut donc dans une certaine mesure s'en passer. De là le développement d'éléments structuraux certes un peu plus complexes mais beaucoup plus légers, tels que:
la poutre en I
On a d'abord fabriqué des poutres en I en métal avant de les faire en bois. Question d'économie pour un matériau au départ cher à produire mais pas trop difficile à profiler. On les trouve de nos jours en abondance dans la charpenterie métallique.
Plus récemment, on s'est mis à faire des poutres en I en bois. Les plus courantes sont constituées de deux membrures en bois massif et d'une âme à base de panneau de particules (type OSB). Leur poids peut être inférieur de 40 % à celui d'une poutre en bois massif de même résistance.
Doubler la hauteur de l'âme permet de multiplier par quatre la charge admissible sans ajouter énormément de matière.
les tubes creux
À quantité de matière égale, un tube creux est beaucoup plus résistant qu'une tige pleine.
Expérience: prenez une feuille de papier A4 ordinaire et collez bord à bord les deux grands côtés avec une fine bande de ruban adhésif. Vous obtenez une colonne d'environ 30 cm de hauteur et 7 cm de diamètre. Posez-la verticalement sur une balance de cuisine et commencez à empiler du poids dessus, tout doucement et bien à plat (des livres conviennent parfaitement). Avant d'allez plus loin, essayez de deviner quel poids cette colonne d'apparence extrêmement fragile va supporter avant de s'effondrer. Reprenez l'empilement de livres jusqu'à ce que ... boum badaboum! Une de mes colonnes en papier a supporté sans broncher 3,4 kg et s'est effondrée à 3,5! Qui dit mieux?
les poutres en treillis
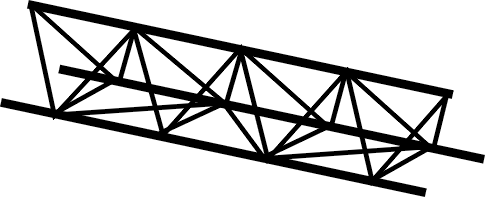
Plus récente que la poutre en I, l'intérêt de cette structure est de résister d'égale manière à des efforts dans toutes les directions, tandis que la poutre en I résiste mal à des efforts perpendiculaires à son âme.
La poutre en treillis est employée dans de nombreuses structures métalliques, à commencer par les grues.
Tout ceci est connu depuis longtemps des ingénieurs et se retrouve dans d'innombrables bâtiments, qui d'ailleurs n'auraient pu être construits sans ces éléments de structure allégés. Le problème est que ça n'a guère fait son chemin chez les architectes de maisons individuelles, et encore moins dans l'esprit de monsieur et madame tout-le-monde. La plupart croient encore naïvement que gros et lourd est forcément synonyme de solide: "Rien ne vaut un mur en pierres, rien ne vaut des poutres en bois massif." En fait c'est surtout synonyme de poids mort et superflu. Il est important de commencer par opérer ce retournement de pensée si l'on veut aller encore plus loin dans l'allègement des structures. En se souvenant qu'il ne s'agit pas de faire de l'allègement pour de l'allègement mais d'aller à l'essence même de la matière (considérée à notre échelle et pas à l'échelle atomique, cela suffit ici) pour être à même de jouer avec.
Dans une poutre soumise à des efforts il y a des parties qui travaillent en tension et d'autres qui travaillent en compression. Les poutres envisagées jusqu'ici sont faites de la même matière. Or il n'y a aucune raison qu'une matière donnée soit aussi performante dans les deux sens.
On sait par exemple que le bois a une excellente résistance à la tension et bien moindre à la compression. Inversement, la pierre et le béton (qui n'est au fond que de la pierre reconstituée) ont une résistance très élevée à la compression mais très faible à la tension. Or comme une poutre soumise à une charge subit à la fois tension et compression, aucun de ces deux matériaux n'apparaît comme idéal. Seule leur abondance explique leur emploi généralisé. Comme ils ne sont pas vraiment adaptés, on a facilement tendance à surdimensionner les éléments porteurs, ce qui ne fait qu'ajouter du poids et donc tend à accentuer les problèmes au lieu de les résoudre. Il suffit de visiter toutes sortes de vieux édifices pour voir des planchers et des toitures avachies qui cachent des poutres de bois fléchies exagérément, fendues, voire cassées. Et quand tout a l'air sain, c'est souvent que des rénovations importantes ont eu lieu, voire des reconstructions complètes, ce qui n'empêche pas de dater l'édifice de plusieurs sicèles. Idem en présence de vieux linteaux de pierre qui sont presque toujours fendus. Ne résistant guère à la tension, un tel linteau se fragilise du côté de la tension maximale, c'est-à-dire dessous. Une fissure apparaît qui peut se propager à toute l'épaisseur et finir par casser la pierre en deux. C'est ce qui limite la portée. Et c'est pour pallier à cette faiblesse que l'on a imaginé d'armer le béton, les tiges en fer noyées dedans servant à le rendre plus résistant à la tension. D'où la possibilité de portées beaucoup plus grandes à épaisseur égale.
Le béton armé est très performant (cf. les immenses portées de certains ponts), bon marché, mais pas vraiment léger car il ne va pas au bout de la logique. La véritable simplification de la poutre passe par la séparation structurelle les lignes de tension et des lignes de compression permettant d'employer pour chacune les matériaux les plus appropriés. Parvenus à ce point, un petit détour est nécessaire pour comprendre ce qui rend une matière résistante à la tension ou résistante à la compression.
Les éléments supportant bien la tension sont des tiges, des câbles ou des chaînes en acier; des cordes en chanvres, en nylon, en kevlar, etc. On y pense moins mais les textiles et autres membranes peuvent aussi constituer d'excellents éléments travaillant en tension. Leur cas sera examiné dans la troisième partie.
Pendant longtemps, les seuls matériaux disponibles ont été tirés des végétaux: cordes de chanvre, de bambou, lianes, etc. On s'en est servi principalement dans la marine et dans une moindre mesure pour réaliser des ponts suspendus. Pas ou peu d'applications en architecture sinon sur les chantiers pour tirer et soulever les charges.
Il faut dire que les quelques 700 kg/cm² de résistance à la traction des fibres végétales ne font guère le poids face aux 4000 kg/cm² de résistance à la compression d'une maçonnerie en pierre. Elles ne supportent pas non plus la comparaison en terme de durée de vie.
Il a fallu attendre le milieu du 19e siècle avec le début de la production en masse de l'acier pour disposer d'un nouveau matériau performant autant en tension qu'en compression, environ 3500 kg/cm² dans les deux sens pour l'acier ordinaire. Sans compter qu'il se travaille aussi bien en fils qu'en plaques qu'en tiges pleines ou creuses.
Dans la conception d'une structure, un autre facteur compte en plus de la résistance du matériau, son élasticité. Si vous suspendez un poids de 100 kg à un câble d'acier de 1 cm de diamètre, son allongement ne sera guère perceptible. Une corde en chanvre de 2,2 cm ayant une résistance à peu près similaire s'allongera davantage. Quant à un ruban de caoutchouc, il s'étirera tant et tant qu'il finira par toucher le sol et ne portera plus aucune charge. Il est évident que les matériaux trop élastiques sont inutilisables dans une structure pour supporter les efforts de tension car cela entraînerait des déformations considérables.
Cet inconvénient est connu depuis longtemps et les hommes ont trouvé le moyen d'y palier dans une certaine mesure: en enroulant un fil sur lui-même puis en enroulant en sens contraire plusieurs fils ensemble (torons formant une corde ou un câble), on diminue notablement l'élasticité du produit final par rapport à l'élasticité du matériau qui le constitue. C'est tout l'art de la corderie.
Pour être plus précis, il faut distinguer trois types de comportement d'un matériau soumis à une tension:
1. comportement élastique: le matériau retrouve exactement sa forme initiale après relâchement de la tension;
2. au-delà d'une certaine tension le comportement devient plastique, c'est-à-dire qu'après relâchement de la tension le matériau conserve une déformation permanente;
3. si la tension augmente encore on atteint le point de rupture.
Pour l'acier par exemple le point de limite élastique est atteint pour un allongement de 0,2% et la rupture se produit pour un allongement de 25%. En comparaison la poterie se brise pour un allongement de 0,5% seulement et le caoutchouc pour un allongement de 300%.
Voici un petit tableau comparatif entre différents matériaux (l'unité de mesure habituelle est le MPa soit 106 N/m² mais comme ce n'est pas très parlant aux néophytes je l'ai convertie en kg/cm²):
|
matériau |
limite d'élasticité |
résistance à la rupture |
|
bois de pin |
400 |
|
|
acier haute résistance |
6900 |
7600 |
|
acier très haute résistance |
16500 |
18600 |
|
aluminium |
950 |
1100 |
|
nylon |
450 |
750 |
|
marbre |
150 |
|
|
polypropylène |
120 à 430 |
200 à 800 |
|
kevlar |
36000 |
Il est moins évident de sentir ce qui rend un élément résistant à la compression. Pour la pierre, la question ne se pose pas tant on est habitué à voir des montagnes s'élever sur des milliers de mètres. Mais qui aurait imaginé qu'une simple feuille de papier très souple d'à peine 5 g et 1/10 de mm d'épaisseur pouvait porter près de 700 fois son poids à 30 cm de hauteur?
Pour essayer d'y voir plus clair, commençons par remarquer une différence majeure de comportement dans une poutre selon qu'elle est soumise à une traction ou à une compression:
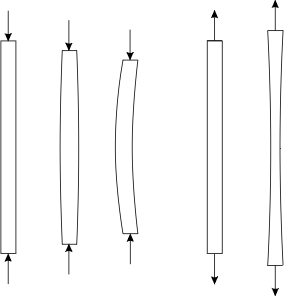
Sur la partie droite de l'images on voit que la poutre ou la tige en traction tend à l'allonger et à s'affiner. Dans ce processus, elle conserve parfaitement son alignement selon l'axe de traction. Notons en passant que cela explique pourquoi un élément travaillant exclusivement en tension n'a pas à être rigide, il peut être souple, comme un câble ou une membrane.
Au contraire, une poutre soumise axialement à un effort de compression va dans un premier temps s'écraser et dans un deuxième temps gauchir jusqu'à se briser (images de gauche). On dit que la poutre flambe. C'est ce qui s'est produit pour ma colonne de papier pour une force de 3,5 kg.
Qu'est-ce qui rend un élément résistant à la compression? Pour comprendre ce qui se passe dans ce domaine plutôt contre intuitif, un petit détour par la science est recommandé.
Euler a trouvé une formule empirique qui permet de connaître approximativement la charge critique à laquelle une longue colonne va s'effondrer. 'Longue' veut dire ici qu'elle fait au moins dix fois le diamètre. Il existe des variantes de cette formule pour des colonnes présentant d'autres caractéristiques, mais cela ne change rien ici car l'on va se contenter d'un raisonnement qualitatif. Voici donc la formule d'Euler:
![]()
où E est un facteur caractéristique du matériau appelé module d'élasticité de Young, I un facteur qui caractérise la forme de la section de la colonne, L la longueur.
Pour faire une tige résistant à la compression, on peut jouer sur ces trois facteurs:
1. le matériau (représenté par E): par exemple à diamètre égal l'acier est plus résistant que le bois;
2. la forme de la section (représentée par I): à quantité de matière égale, un tube de grand diamètre et de faible épaisseur (jusqu'à une limite permise par le matériau) est plus résistant qu'un tube plus petit mais plus épais; c'est ce qui rend une colonne de papier aussi résistante malgré un facteur E très défavorable; idem pour les tiges de bambou et autres graminées;
3. la longueur (L): un facteur crucial dans la mesure où il intervient dans la formule par son carré; autrement dit, diviser la longueur par deux multiplie la résistance par quatre.
Voici par exemple comment on fait en sorte qu'un mât de voilier, bien que d'un seul tenant, puisse être considéré du point de vue structurel comme un assemblage de deux poutres plus courtes donc beaucoup plus résistantes:
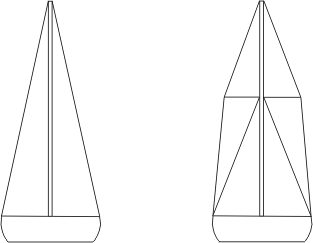
Ce dernier exemple que les marins ont découvert empiriquement il y a déjà longtemps nous donne une idée de la façon de séparer dans une poutre les éléments de structure qui travaillent en compression de ceux qui travaillent en tension.
Si les efforts s'exercent principalement dans une seule direction, la solution la plus simple consiste à rajouter du côté opposé une petite tige travaillant elle aussi en compression et supportant un câble en tension:
L'élément principal qui supporte la compression peut être une simple poutre ou bien une poutre en I ou encore un tube métallique, toutes les combinaisons sont possibles.
On devine que lorsqu'une charge est appliquée sur la poutre, elle est reprise par les câbles qui se tendent. Il est important que la tige intermédiaire soit assez longue pour que l'angle A soit assez ouvert (empiriquement on considère qu'il faut au moins 9°) car la tension sur le câble est proportionnelle à l'inverse de son sinus (voir plus haut § le poids). Mais il ne doit pas non plus être trop ouvert sinon la diminution de la tension du câble est contrebalancée par une augmentation du risque de rupture de la tige intermédiaire devenue trop longue (rappelons que, soumise à des efforts de compression, sa résistance diminue avec le carré de sa longueur). Tout est donc affaire de compromis.
Voici une variante pour une poutre soumise à des efforts dans toutes les directions:
Comment font les arbres, qui se comportent comme des grands mâts non haubanés, pour résister aussi bien au vent? Car il faut vraiment une grosse tempête pour casser un arbre. D'ailleurs il est plus fréquent qu'il soit déraciné que cassé.
La première raison est que le tronc est plus gros à la base qu'au sommet, de sorte qu'il est plus résistant là où les efforts sont les plus grands.
L'autre raison est plus subtile. Le cœur d'un arbre est constitué de bois mort. La partie vivante, celle où circule la sève, est une couronne située à la périphérie appelée aubier. Les fibres de l'aubier présentent la particularité d'être déjà sous tension, en s'appuyant sur le bois du cœur. Lorsque le vent souffle et que l'arbre se courbe, on sait que les fibres sur la face interne (ici du côté opposé à la direction du vent) se raccourcissent. Mais elles ne se retrouvent pas immédiatement en compression car dans un premier temps c'est simplement l'excès de tension naturelle qui est absorbé par le raccourcissement (comme un élastique tendu que l'on relâche un peu). Une compression n'apparaît que plus tard lorsque la courbure s'accentue. De ce fait, il faut une amplitude beaucoup plus grande pour que la relative faiblesse en compression des fibres de bois se manifeste.
Quant aux côté au vent, il va subir une tension encore plus forte que la normale du fait de la pré-tension, mais c'est sans conséquences dans la mesure où le bois est justement très résistant à ce genre d'effort.
Le centre de l'arbre pour sa part, qui n'est que du bois mort, se trouve comprimé par la pré-tension de l'aubier. Cette compression ne devient pas excessive lorsque le tronc se courbe puisque le cœur se situe dans la zone neutre sans grande tension ni compression. D'ailleurs un arbre creux reste solide et peut vivre encore longtemps.
Tout ceci explique la grande résistance d'un arbre vivant. Ceci explique aussi pourquoi un arbre mort risque de casser beaucoup plus facilement lors d'un coup de vent. Faiblesse en apparence paradoxale puisqu'il subit des efforts moindres, ayant déjà perdu une partie de sa ramure et tout son feuillage.
On voit sur cet exemple comment la Nature joue avec les forces de tension et de compression. Elle crée une structure extrêmement résistante avec une grande économie de moyens puisque ce sont deux états du même matériau (le bois vivant plus souple et tendu, et le bois mort moins souple mais plus dur) qui absorbent les différentes contraintes. Les fibres de l'aubier constituent une sorte de gaine en tension autour d'un cœur en compression.
Remarquons en passant qu'on ne bénéficie pas du tout de ces avantages lorsqu'on emploie le bois comme matériau de construction car il n'est plus vivant et par conséquent son comportement à l'effort ne saurait se comparer à celui d'un arbre vivant mais plutôt à celui d'un arbre mort.
Une gaine en tension enserrant un cœur en compression, voilà qui rappelle le principe des structures gonflables. Sauf qu'à la différence de l'arbre, on se sert ici de deux matériaux différents: de l'air sous pression enfermé dans une membrane étanche sous tension, en forme de cylindre s'il s'agit de reconstituer une poutre ou de la moitié d'un tore pour une arche. Une telle structure est un cas idéal de parfaite séparation entre l'élément travaillant en compression et l'élément travaillant en tension.
Il y a juste un petit problème qu'on a déjà rencontré à propos de l'arche gonflable, c'est la faible capacité portante d'une telle structure. Elle est due essentiellement au caractère fluide de l'air et à sa grande compressibilité. Dans le cas de la poutre gonflable, on dispose d'une formule reliant la charge linéique q qu'elle est apte à supporter, la pression p, et le rapport c entre la longueur et le diamètre:
![]()
Si l'on veut que la poutre supporte un tant soit peu de poids, il faut une pression élevée et surtout un très faible facteur c . Mais peut-on encore considérer que l'on a une poutre lorsque le diamètre se rapproche de la longueur? S'il est facile de faire un ballon qui supporte le poids d'un homme, c'est beaucoup plus difficile de faire une poutre.
Finalement, si un tel élément de structure apparaît idéal du point de vue conceptuel, il l'est beaucoup moins en termes de performances. Pas découragés pour autant, des chercheurs ont persévéré. Remettant le problème complètement à plat, ils sont parvenus à une solution remarquable qui constitue à ce jour le meilleur compromis performance-légèreté.
Le nom tensairity est construit sur tension + air + integrity. Ses concepteurs l'ayant déposé, je ne le francise pas. C'est un tout nouveau principe structurel d'une simplicité, d'une élégance, d'une légèreté et d'une efficacité remarquables. Il prouve s'il en était encore besoin que l'ère des découvertes dans ce domaine n'est pas révolue. Il est le fruit très récent d'une dizaine d'années de recherches sur les structures pneumatiques, principalement de la part de Rolf Luchsinger (Prospective Concepts ag, http://www.propective-concepts.ch) et Mauro Pedretti (Airlight Ltd, http://www.airlight.biz).
Il consiste à utiliser un coussin d'air pour rendre plus résistant à la flexion un élément travaillant en compression. Une poutre en tensairity comprend trois éléments intimement reliés:
1. un long coussin (en polyester enduit de PVC, tissu de verre enduit de Téflon, tissu de verre enduit de silicone, etc.), ici de forme cylindrique, gonflé à une pression allant de 50 à 500 g/cm²;
2. une tige rigide (en bois, acier, aluminium, etc.) épousant le coussin sur toute sa longueur;
3. deux câbles (en acier ou autres) reliant les extrémités de la tige en s'enroulant en spirale autour du coussin.
La charge est portée par la tige et les câbles. La fonction de l'air comprimé est de mettre les câbles sous tension, ce qui stabilise l'élément en compression et réduit sa flexion. C'est pourquoi sa section peut être notablement réduite par rapport à une poutre porteuse traditionnelle. On obtient ainsi un ensemble d'une grande rigidité tout en restant très léger. Tous les éléments sont employés à leur optimum, autant ceux qui travaillent en tension (c'est déjà le cas dans les structures tendues) que ceux qui travaillent en compression (c'est rarement le cas).
Notons que les risques d'effondrement sont négligeables même en cas de percement de la membrane. Les concepteurs ont calculé que, sous une pression de 100 g/cm², l'énergie nécessaire pour remplacer l'air qui fuit par un trou de 6 mm de diamètre n'est que de 1 W.
Quant aux pertes d'air par porosité d'une membrane faite de tissu de verre enduit de silicone, elles ne s'élèvent qu'à 5 litres par mètre carré et par an.
L'affaiblissement de la structure par perte de pression est un processus lent qui laisse le temps d'intervenir. Et en cas de destruction totale du coussin, la structure tient encore puisqu'il y a un élément porteur rigide, même si elle n'est plus capable de supporter d'autres charges que son propre poids.
Le principe a été appliqué pour la première fois à un pont prototype de 8 m de portée capable de supporter une charge maximale de 3,5 tonnes.
 |
http://www.airlight.biz |
La structure est constituée de deux poutres en tensairity:
1. chaque coussin a la forme d'un cylindre de 50 cm de diamètre, en polyester-PVC, gonflé à 400 g/cm²;
2. les tiges sont en carbone, mais de l'acier ou de l'aluminium auraient convenu tout autant;
3. les câbles sont en acier de 6 mm de diamètre; une paire supplémentaire s'enroulant deux fois autour du coussin a été ajoutée pour prendre en compte le fait que la charge (voiture ou camion) se déplace;
4. des planches recouvrent transversalement les deux poutres, sans autre fonction que de servir de voie de roulement.
Une poutre complète pèse 40 kg. Une poutre en acier de même capacité portante pèserait 370 kg. Quant à une poutre gonflable équivalente, elle nécessiterait une pression d'environ 15 kg/cm² (pression régnant à 150 m sous la mer! pour mémoire les pneus d'une voiture de tourisme sont gonflés aux environs de 2 kg/cm² seulement).
Outre l'avantage du poids, le pont peut être monté et démonté très rapidement.
 |
http://www.airlight.biz |
Tout récemment, en 2005-2006, le procédé a permis la réalisation d'un ouvrage remarquable à Lanslevillard, dans le cadre de la station de ski de Val Cenis: 52 mètres d'une seule portée et 8 mètres de largeur.
 |
http://www.airlight.biz |
Ce pont permet aux skieurs d'accéder directement depuis le village au domaine skiable. Des charges importantes ont dû être prises en compte: 1,5 tonnes de neige par mètre carré, plus le poids des skieurs, plus celui des engins de déneigement, soit au total des charges réparties supérieures à celles que supporte un pont autoroutier calibré pour le franchissement de 40 tonnes!
Le matériau principal est du mélèze local, 220 mètres cubes en lamellé-collé, à quoi s'ajoutent 30 tonnes de métal pour les tirants, les pièces de liaison et autres. L'ensemble acquiert sa résistance grâce à deux grands coussins en tensairity gonflés à 200 g/cm², représentant 850 mètres carrés de membranes en tissu de verre enduit de silicone.
Si l'on sait faire de tels ponts, il est facile d'imaginer que l'on puisse faire aussi des toits.
Même si c'est un peu compliqué, cela vaut le coup d'essayer de comprendre comment ça marche (les informations de ce paragraphe sont reprises pour l'essentiel de l'article de Mauro Pedretti: http://www.imamod.ru/~serge/arc/conf/ECCOMAS_2004/ECCOMAS_V2/proceedings/pdf/959.pdf).
Comparons une poutre en tensairity (en haut sur le dessin) à une poutre classique renforcée par un câble et des tiges verticales (en bas):
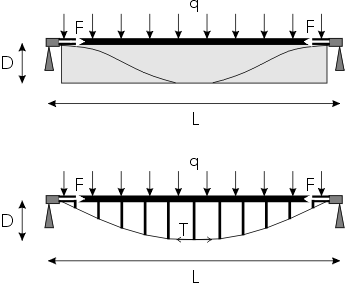
L est la longueur, D la hauteur (et aussi le diamètre du coussin), q la charge linéaire uniforme, T la tension du câble, p la pression dans le coussin.
Dans ces deux types de structures, la flexion de la poutre sous l'effet d'une charge met le câble en tension, ce qui limite la déformation. Si l'on considère g =L/D très grand, on a:
![]()
Cette tension est reprise à son tour par la poutre au niveau de ses extrémités où elle exerce une force de compression. Notons F la charge de flambage sous flexion qu'elle peut supporter. Elle vaut dans le cas d'une poutre classique comportant n tiges verticales (variante de la formule d'Euler pour une poutre simple vue précédemment) :
![]()
où E est le module d'élasticité de l'élément en compression et I son moment d'inertie (je rappelle que le premier caractérise le matériau, le second la forme).
La présence dans la formule de l'inverse de la longueur au carré signifie que la capacité de la poutre à supporter la flexion diminue très vite avec sa longueur.
La poutre en tensairity quant à elle se comporte comme si elle était soutenue élastiquement sur toute sa longueur. Dans ces conditions:
![]()
Le fait remarquable est que la longueur L a complètement disparu de la formule. Cela signifie que le moment de flexion de l'élément en compression est indépendant de la portée. C'est ce qui rend le procédé si efficace même pour des très longues portées.
La formule qui relie la pression p à la charge linéique q est elle aussi indépendante de la longueur pour la poutre en tensairity:
![]()
En comparaison, la formule pour une structure gonflable cylindrique (sans tige ni câble donc, comme un boudin de canot pneumatique par exemple) vaut:
![]()
Le facteur g ² est responsable du fait que la pression 'explose' dans une structure gonflable lorsque la portée augmente. À titre d'exemple, si l'on prend g =16 (je rappelle que c'est le rapport longueur / diamètre, par exemple 8 mètres de long pour un diamètre de 50 centimètres) alors la pression dans une simple poutre gonflable est 33 fois plus élevée que celle requise dans une poutre tensairity pour la même capacité portante. Et elle est plus de 100 fois plus élevée pour g =30. Il n'est pas courant qu'une nouvelle technologie apporte un gain d'un tel facteur.
Ajoutons encore que de légères modifications de la forme du coussin apportent de nouveaux gains de performances. Quatre formes ont été étudiées: cylindre, cigare, fuseau symétrique et fuseau asymétrique.
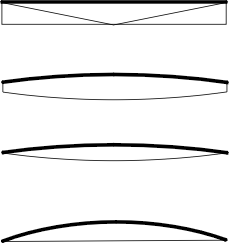
Remarquons que dans les trois dernières formes la tige est courbée en arc et que dans la toute dernière le câble est droit et non plus en spirale.
À titre de comparaison, voici l'effet d'une charge de 150 kN:
|
forme |
déflection centrale |
|
cylindre |
50 cm |
|
cigare |
25 cm |
|
fuseau symétrique |
12 cm |
|
fuseau asymétrique |
10 cm |
Les structures porteuses en tensairity fonctionnent avec une pression intermédiaire entre les structures supportées par l'air (au plus quelques grammes par centimètre carré) et les structures gonflables (où la pression se compte en centaines voire en milliers de grammes). Toutefois même 100 g/cm² imposent à la membrane des contraintes importantes et exigent une grande qualité de fabrication. Je ne sais si c'est accessible à un bon bricoleur, même en se limitant à la forme la plus simple, le cylindre. Je ne sais pas non plus s'il pourrait se dépatouiller des problèmes de dimensionnement. Quoiqu'il en soit la démocratisation de cette idée mériterait d'être étudiée car elle va dans le sens de structures porteuses légères, solides, rapides à monter et démonter.
Commençons par rappeler quelques défis que l'architecte (patenté ou non) doit relever:
- créer une séparation matérielle entre un espace intérieur et l'espace extérieur, par opposition à des volumes purement sculpturaux comme sont des édifices tels que les pyramides, certains temples hindous, ou, formes en creux, les cavernes;
- cette forme matérielle délimite un volume 'habitable', les guillemets indiquant les grands écarts de sens que peut avoir ce terme, de l'abri d'une nuit pour une seule personne à d'immense halls pouvant contenir des foules entières en passant par l'espace de vie et/ou de travail d'une famille;
- ce volume est organisé principalement selon des surfaces planes et horizontales pour permettre à l'habitant de s'y mouvoir aisément, car il s'agit ici d'une architecture terrestre par opposition à une architecture spatiale pour une vie en apesanteur;
- la forme est soutenue par une structure apte à résister pour une durée plus ou moins longue (de moins d'une journée pour se protéger d'une tempête à plusieurs générations) à toutes sortes de forces entropiques qui s'acharnent à la disloquer (surcharges pondérales, rafales de vent, tremblements de terre...) ou à la décomposer (action de l'eau, des ultraviolets du Soleil, des écarts de températures extrêmes...).
Passé le temps de la grotte, les hommes ont développé différents procédés constructifs pour répondre à ces défis. Le problème était de créer les surfaces délimitant ces volumes à partir de matériaux se présentant soit sous forme de petits volumes (pierres, briques, etc.), soit sous forme linéaire (troncs, branches, lianes, etc.). De là les deux grands procédés constructifs:
1. les empilages: on empile des matériaux qui se présentent comme des petits volumes et qui travaillent essentiellement en compression pour recréer en quelque sorte la grotte avec son côté massif et ses ouvertures étriquées: c'est tout l'art de la maçonnerie;
2. les assemblages: on fabrique des cadres rectangulaires rigides avec des éléments linéaires travaillant en flexion (combinaison de tension et de compression) dont les surfaces sont comblées ensuite avec toutes sortes de matériaux (ou non: cf. les huttes des pays tropicaux où seul le toit est couvert et où les murs restent ouverts): c'est tout l'art de la charpenterie.
Remarquons que les deux procédés ne sont pas incompatibles et sont même fréquemment combinés. Ainsi des murs construits selon le premier procédé ont souvent pour toiture une structure construite selon le deuxième.
L'incapacité des structures empilées à résister à d'autres force que la gravité a déjà été évoquées. Ce n'est pas le seul de leurs défauts. Un autre est que le catalogue de formes est plutôt restreint, avec des ouvertures étriquées, à moins de panachage avec des techniques modernes (poutres en béton armé par exemple) ou de prouesses dont seuls sont capables quelques artisans parvenus à une grande compréhension de la matière: cf. les cathédrales gothiques, les châteaux de la Renaissance, les œuvres de Gaudi, etc.
Autre défaut déjà évoqué, l'extrême lourdeur de toute la chaîne de production puisqu'il faut bien extraire et amener sur le chantier ces tonnes et ces tonnes de matériaux.
Ajoutons que même si les matériaux employés sont directement tirés de la terre, cela ne fait pas de ces édifices des ˝structures naturelles˝. Au contraire, tant par leur forme que par leur structure, leur artificialité saute aux yeux.
Il est par ailleurs intéressant de noter à quelle vitesse la Nature transforme en ruines des bâtiments non entretenus. Comme si elle voulait les effacer au plus vite du paysage, elle les érode, les disloque, les effondre, sans toutefois parvenir à les digérer complètement puisque longtemps subsistent des cicatrices disgracieuses.
Ce n'est pas qu'il faille absolument s'interdire d'utiliser ces procédés de construction. Rien n'est à interdire. Tout est affaire de sens. N'importe quel procédé a sa valeur à condition de l'employer de manière sensée et non pas dogmatiquement ou faute de mieux ou parce que on ne veut pas apprendre à faire autrement. Les empilages sont imbattables lorsqu'il s'agit de construire à faible coût des structures capables de résister à des charges pondérales très élevées. Par exemple, si l'on a besoin d'une pièce qui doit garder une température constante tout au long de l'année, une voûte recouverte d'une épaisse couche de terre est préférable à tout autre structure. De même la maçonnerie s'impose pour des usages spécifiques tels que citernes pour l'eau potable, etc.
Bref, l'emploi de ce procédé comme de n'importe quel autre doit toujours avoir un sens. Quant aux détails techniques, je n'insiste pas car c'est pratiquement à la portée de n'importe qui tant qu'on reste dans des dimensions raisonnables. Preuve en est les innombrables fermes de pierres réalisées en autoconstruction qui balisent les campagnes de nos pays, ou les maisons plus récentes en briques ou en parpaings qui ne réclament pas beaucoup de compétences en maçonnerie.
Mais si l'on veut aller plus loin, concevoir une architecture qui soit plus variée quant aux formes possibles, plus légère à tous points de vue, et structurellement mieux conçue, il faut, au risque de me répéter, apprendre jouer avec les deux forces complémentaires de tension et de compression.
Cet autre procédé constructif est plus intéressant car plus léger (relativement), plus riche quant aux formes possibles, et structurellement plus abouti. C'est tout l'art de la charpente, qu'elle soit en bois (arbres ou bambous) ou métallique, qu'elle soit traditionnelle (poutres de bois massif, plaques d'acier rivetées...) ou moderne (poutres de bois lamellé-collé, poutres en I, tubes d'acier ou d'aluminium boulonnés...).
Le procédé et toutes ses variantes ont largement fait la preuve de leurs possibilités, tant en termes de formes, de résistance, de dimensions, de durée:
- cf. tous les immenses toits de châteaux et de cathédrales réalisées par des compagnons charpentiers;
- cf. les prouesses de la charpenterie métallique dès le 19e siècle avec des réalisations telles que: gares, immenses halls d'expositions (Crystal Palace de Londres, Grand et Petit Palais de Paris...), ouvrages d'art (viaducs, ponts, tour Eiffel...), etc.;
- cf. des développements plus récents permis par des nouveaux matériaux comme le lamellé-collé (le plus grand pont routier du monde en bois, le pont de Flisa en Norvège, mesure plus de 181 m de long).
La technique est si bien maîtrisée qu'elle est aujourd'hui largement démocratisée:
- cf. le développement des maisons à ossature bois, y compris en autoconstruction (depuis toujours en Amérique, plus récemment en Europe);
- cf. le succès des vérandas, qui doit beaucoup à l'essor des éléments de charpente en aluminium;
- cf. les innombrables bâtiments utilitaires tels que granges, ateliers, entrepôts, centres commerciaux, etc., construits en charpente métallique ou en lamellé-collé...
Tout ça n'est pas toujours le summum du bon goût ni du confort, mais là n'est pas mon propos dans ce chapitre. L'important ici est de constater que ce procédé constructif, qui ne consiste au fond qu'en assemblage de poutres, est largement éprouvé et désormais accessible à de nombreuses personnes sans formation d'ingénieur.
Dans ce procédé constructif, on part d'éléments simples, quasi linéaires, que l'on assemble de manière appropriée pour créer des cadres rigides, lesquels constituent en quelque sorte l'ossature d'une forme sur laquelle viendra ultérieurement se greffer une peau. Plutôt que de peau il vaudrait peut-être mieux parler de carapace ou d'armure dans la mesure où elle n'est pas sensible (comme l'est a contrario une membrane) ni organiquement reliée à la structure.
Remarquons que d'un point de vue purement géométrique une telle structure n'est qu'un assemblage de lignes. L'épaisseur ou le diamètre des éléments n'ont quant à eux aucune fonction géométrique et ne sont déterminés que par la résistance qu'ils doivent avoir en fonction des contraintes à supporter. Autrement dit, il y a dans une certaine mesure découplage entre les différentes caractéristiques dimensionnelles de l'élément, c'est-à-dire entre la longueur d'une part qui a une fonction géométrique de délimitation de la forme, et l'épaisseur d'autre part qui est fonction des efforts s'exerçant sur cet élément (et qui dépend aussi de la longueur bien évidemment, cf. plus haut la formule d'Euler).
C'est parfaitement visible sur un édifice comme la tour Eiffel. De loin, on voit seulement des grandes lignes qui délimitent une forme unique en son genre. De près, la forme générale s'efface, l'épaisseur des éléments apparaît en tant que facteur de résistance de la structure ainsi que l'enchevêtrement d'entretoises qui visent à rigidifier l'ensemble. On remarque en particulier que plus les éléments sont courts, plus ils sont nombreux et moins ils sont épais. On remarque aussi la présence d'innombrables triangles, même lorsque la forme finale n'est pas triangulaire, qu'elle est ronde, carrée, trapézoïdale ou autre.
Pour ceux qui ne s'en souviendraient plus, je profite de l'occasion pour rappeler le principe de la triangulation. Il repose sur le fait que trois tiges assemblées en triangle constituent géométriquement un assemblage indéformable. Cela vient du fait qu'un triangle est entièrement défini par la longueur des trois côtés, c'est-à-dire que les trois angles aux sommets ont une valeur unique. Un angle ne peut pas changer si un côté ne change pas.
Cette indéformabilité du triangle est très facile à vérifier. Prenez trois tiges, trois morceaux de bois par exemple ou trois stylos, et attachez-les bien ensemble (quelques tours de ruban adhésif peuvent suffire). Si vous poussez sur un côté ou sur un angle, l'ensemble tourne d'un seul bloc, sans se déformer, c'est-à-dire que le triangle reste identique à lui-même. À comparer avec le comportement d'un rectangle qui tend naturellement à se déformer en losange, déjà sous son propre poids sans qu'il soit même besoin de pousser:

La solution pour le rigidifier consiste à le trianguler. Il y a plusieurs manières de faire:

Dans le premier cas (à gauche), une tige rigide placée en diagonale partage le rectangle en deux triangles indéformables. Elle contrarie les déformations vers la droite en se mettant en tension et vers la gauche en se mettant en compression.
Dans le second cas (au milieu), on triangule chaque angle de la structure avec des tiges.
Dans le troisième cas (à droite), on utilise des câbles en diagonales. Un seul ne suffit pas du fait qu'il ne travaille qu'en tension. Il en faut deux pour que chacun absorbe un type de déformation.
En architecture, cela donne lieu à d'innombrables variantes, telles que:
 |
 |
Répété, le procédé permet de construire de grandes structures indéformables.
Entendons-nous bien: 'indéformable' porte ici uniquement sur la géométrie, car il est bien évident que la structure peut toujours se déformer en fléchissant sous l'action de forces plus ou moins importantes. Reprenez le triangle que vous avez réalisé tout à l'heure et exercez une forte pression sur deux angles ou sur deux côtés ou sur un angle et le côté opposé. Si les tiges ne sont pas surdimensionnées par rapport à votre capacité musculaire, elles devraient fléchir. Quant à un rectangle triangulé, il peut en plus se déformer en dehors du plan, comme si on tirait sur deux sommets opposés pour les rapprocher.
C'est dans ce passage de la géométrie à la structure qu'intervient la question du dimensionnement de chaque élément pour que, soumise aux efforts maximaux que l'on se donne a priori, sa déformation reste élastique.
L'ossature que constituent ces assemblages délimite des surfaces qui délimitent des volumes. Les surfaces, qui peuvent rester ouvertes dans le cas des ouvrages d'art, doivent être fermées dans la plupart des autres cas, au moins au niveau du toit, et aussi le plus souvent au niveau des murs. Tous les matériaux possibles sont utilisés pour boucher les trous:
- murs et toits en branches ou feuilles tressées (huttes, toits de chaume, de roseaux, de feuilles de palmier...);
- murs et toits en bardeaux de bois, d'écorces, de bitume;
- murs en terre, torchis, pierres ou briques employées en comblement sans fonction portante;
- toits de pierres (lauzes, ardoises), de terre cuite (tuiles), de métal (zinc, tôle ondulée, bacs acier...);
- membranes souples en peaux de bêtes, tissus ou tapis de laine pour les tentes traditionnelles, en toiles de coton, polyester, vinyle ou nylon pour les tentes plus récentes;
- plaques transparentes de verre, de polycarbonate ou d'acrylique;
- etc.
L'important à remarquer est que ces éléments de comblement participent peu voire pas du tout à la structure. Au contraire ils viennent se surajouter comme des poids morts qui de surcroît offrent prise au vent. Finalement ils ne constituent la plupart du temps qu'une lourde carapace qui vient recouvrir une ossature rigide.
Une chose frappe lorsqu'on regarde un bâtiment en train de se construire, l'apparente légèreté de l'échafaudage par rapport au bâtiment lui-même. Il semble même fragile alors qu'il est capable de supporter des vents violents et de soutenir des charges élevées.
En regardant plus attentivement, on remarque une importante différence de conception dans leur structure: le bâtiment, en supposant qu'il soit un assemblage, le sort des empilages étant considéré comme définitivement réglé, est constitué d'éléments de longueurs et d'épaisseurs variées, tandis que l'échafaudage est réalisé à partir d'éléments quasi identiques. Le premier est une structure hiérarchisée, le second une structure non hiérarchisée.
Dans les structures hiérarchisées, des éléments primaires supportent des éléments secondaires qui à leur tour supportent des éléments tertiaires etc. Par exemple: on pose un plancher sur des solives qui reposent sur des poutres accrochées à des poteaux; ou bien on pose des tuiles sur des liteaux fixés à des chevrons reposant sur des panes reposant sur les arbalétriers; ou encore on assemble des poutres de longue portée et de forte épaisseur à l'aide d'entretoises plus courtes et moins épaisses.
D'une manière générale, plus on monte dans la hiérarchie, plus les éléments sont nombreux, courts, et de moindre épaisseur. D'autre part, l'ordre de la construction suit l'ordre de la hiérarchie, d'où la nécessité de passer, repasser et rerepasser maintes fois au même endroit (sans compter le remplissage ultérieur des surfaces puis les multiples couches de peinture, de verni ou de lazure).
Malgré l'efficacité des assemblages hiérarchisés, aussi bien en autoconstruction (huttes, maisons à colombage, à ossature bois, etc.) que pour des réalisations monumentales (hangars, salles de sports, ouvrages d'art, etc.), on commence à en percevoir les limites:
- lourdeur, certes moindre que dans le cas des empilages, mais qui n'est pas négligeable puisqu'à chaque niveau on accumule des matériaux, le tout reposant au bout du compte sur le niveau primaire qui doit être extrêmement costaud;
- grande difficulté de démontage: cf. le nombre de clous, de vis, de tire-fonds, de rivets etc.; quand le bâtiment a vécu, le plus simple est de le démolir et ce qui reste est difficile à réemployer;
- rigidité excessive du fait que chaque niveau participe à la rigidification du précédent; je dis qu'elle est excessive parce que, combinée avec la lourdeur, elle rend l'édifice peu résistant à des efforts de torsion et de cisaillement dus à des vents violents, des tremblements de terre ou tout simplement des instabilités du sol.
Remarquons que cette hiérarchie n'est pas comparable avec ce que l'on observe chez certains êtres vivants comme les arbres. Certes, l'organisation tronc - branches principales - branches secondaires - etc. peut donner l'impression d'une hiérarchie. C'est trompeur. En fait il ne faut pas s'arrêter à un instantané, il faut voir l'arbre dans son processus de croissance. Alors une petite branche apparaît comme une grosse branche en devenir, tandis qu'un liteau ne sera jamais le résultat de la croissance d'un chevron.
L'observation des échafaudages suggère une autre manière de concevoir des assemblages. Il s'agit cette fois de partir de tiges plus légères, plus nombreuses et quasi identiques, et de les assembler en un réseau non hiérarchisé pour constituer directement des surfaces portantes. Bien que la technique des échafaudages existe depuis fort longtemps (en Asie, les bâtisseurs se servent même toujours d'immenses échafaudages en bambou pour construire des immeubles de grande hauteur), l'idée d'étendre le procédé aux bâtiments eux-mêmes est plus récente. C'est avec elle que nous allons pénétrer maintenant dans l'univers des structures légères.