|
|
Bien que disponible gratuitement pour que tout le monde y ait accès sans barrière, ce document n'est pas pour autant sans valeur. Vous pouvez participer aux frais de création et de diffusion, en vous rendant à la page contact.
La logique constructive des assemblages non hiérarchisés est complètement différente de celle des assemblages hiérarchisés. Au lieu de partir d’éléments porteurs grands et lourds autour desquels se construit progressivement la forme, on part de la forme que l’on structure à l’aide de nombreux éléments similaires reliés entre eux. Chacun pris séparément est peu résistant comparé à une poutre porteuse, mais leur nombre et la manière dont ils sont reliés assurent une distribution des efforts sur tous.
|
assemblages hiérarchisés |
assemblages non hiérarchisés |
|
- poutres porteuses peu nombreuses, grandes et fortes; éléments secondaires plus nombreux, plus courts et moins résistants |
- tiges nombreuses quasi identiques |
|
- les éléments d’un même niveau ne sont pas tant reliés entre eux que fixés à des éléments du niveaux inférieur |
- les éléments sont reliés entre eux par des connecteurs qui jouent un rôle structurel majeur |
|
- les efforts sont canalisés vers les éléments du premier niveau |
- les efforts sont distribués dans toute la structure via les connecteurs |
|
- la forme diffère de la structure |
- la forme se confond avec la structure |
Ce dernier point est particulièrement important. Il signifie que la résistance du bâtiment provient entièrement de sa forme. D’où, entre autres, une grande économie puisqu’il n’y a pas à construire deux fois, la structure d’un côté, la forme de l’autre.
Si l’on cherche des précédents à l’emploi de cette logique constructive, ce n’est pas tant du côté des échafaudages évoqués plus haut qu’il faut se tourner que du côté de certains habitats nomades. Question probablement de disponibilité des matériaux, de transportabilité et de facilité de montage/démontage.
De nombreux peuples nomades construisent des huttes simplement en tressant et en attachant des branches fines. Par exemple les Gabras du nord Kenya.

La matière première est relativement facile à se procurer même dans ces régions semi-désertiques (il s’agit en général de fines branches d’acacia), l’ensemble se monte et se démonte rapidement et se transporte sur un chameau.
Plus aboutie sur le plan structurel est la yourte mongole (appellation consacrée venant du russe tandis que les mongoles eux-mêmes l’appellent ger, que l’on voit parfois écrit gher).
La yourte est une construction autoportante c’est-à-dire qu’elle tient toute seule sans avoir besoin d’être ancrée et sans avoir besoin d’un mât planté dans le sol. La structure est constituée d’éléments nombreux mais relativement courts et légers, ce qui la rend facile à transporter. Une yourte de taille moyenne peut se monter et se démonter en une heure à trois personnes. Sa forme ronde et son profil bas la rendent extrêmement résistante aux vents forts de la steppe. Le confort n’est pas en reste de par ses dimensions (de 5 à 10 m de diamètre), son épaisse couverture de feutre en laine de mouton ou en crin de cheval, et la possibilité de faire du feu dont la fumée s’évacue par une petite ouverture sommitale (outre l’intérêt de réchauffer, il maintient la membrane sèche et l’empêche de moisir).
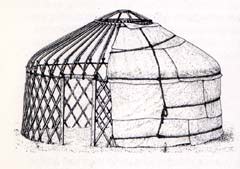
De nombreux occidentaux aspirant à des modes de vie plus simples et plus proches de la Nature ont découvert la yourte ces dernières années (à la suite du tipi). Certains l’achètent, quelques uns se la fabriquent eux-mêmes. On trouve sur internet de nombreux sites donnant des informations pratiques. Je ne discuterai pas ici de l’intérêt de transplanter cet habitat hors de son contexte géographique, climatique et culturel, cette question sera abordée dans le livre 3. Pour le moment un seul point m’intéresse en rapport direct avec mon présent propos, la manière dont est construit le mur, appelé hana ou khana.
Traditionnellement il est fait avec de jeunes pousses d’arbres, de fines tiges coupées à la même longueur, environ 2,5 m. Il en faut une cinquantaine voire plus pour une petite yourte de 5 m de diamètre. Chaque tige est attachée à cinq ou six autres (c’est fonction de leur longueur et de leur nombre) à l’aide de lanières de cuir pour former une structure en treillis à mailles carrées. Le résultat ressemble à ces treillis en bois ou en plastique que l’on trouve dans les jardineries pour palisser les plantes:

Si vous en avez un sous la main, vous constaterez qu’il se courbe très facilement:

Idem pour le khana de la yourte. Les lattes sont assez souples pour que le treillis, une fois posé verticalement au sol, puisse être courbé en cercle. Les extrémités ne sont pas directement attachées mais fixées de chaque côté d’un cadre rigide qui sert d’entrée. Le mur est ceinturé à l’aide de fortes sangles pour bien le maintenir vertical, en particulier pour contrebalancer les forces d’écartement causées par le poids du toit qui repose directement sur le treillis, sans le soutien d’un mât central (dans les petites yourtes du moins, un mât est nécessaire pour les plus grands diamètres).
Cette brève description suffit pour se faire une idée du fonctionnement de cette structure. On comprend en particulier que son intégrité n’est pas remise en cause par la défaillance d’un élément. Une attache peut lâcher, une latte se briser, il y a suffisamment de redondance pour que l’ensemble tienne bon.
Le problème avec ces structures non hiérarchisées simples est qu’elles butent très vite sur des limites dimensionnelles. Cela dépend bien sûr des matériaux et des techniques choisis mais il est évident qu’au-delà de quelques mètres de diamètre force est de rajouter des éléments porteurs classiques tels que poteaux et poutres si l’on veut que cela tienne.
Les limites des structures non hiérarchisées seraient-elles déjà atteintes? Vous vous doutez que non sinon je ne vous aurais pas conduit jusqu’ici. Vous vous doutez également que le passage de la hutte à des structures couvrant des centaines voire des milliers de mètres carrés ne se fera pas sans quelques sauts conceptuels. Sinon ça se saurait, les grands maîtres es structures architecturales des temps passés nous auraient déjà gratifiés de quelques édifices monumentaux de ce genre.
Les avancées sont relativement récentes, première moitié du 20e siècle pour certaines, seconde moitié pour d’autres. Des chercheurs, ou il serait plus exact de dire des trouveurs, ont imaginé des solutions efficaces tout à fait originales. Pour pénétrer à notre tour les principes des coques en treillis de bois, des dômes géodésiques et de la tenségrité, il va nous falloir rompre avec la façon habituelle d’aborder l’architecture. C’est en effet une toute autre manière de penser le rapport de la forme et de la structure, une toute autre manière de construire aussi.
À première vue, on devine deux directions de développement des structures non hiérarchisées:
1. soit on utilise des tiges longues et flexibles que l’on courbe pour former la structure, extension à l’ensemble du bâtiment du principe du mur de la yourte (notons en passant que celle-ci n’a pas une structure homogène puisque son toit est fait de poutres);
2. soit on utilise des tiges plus courtes et rigides assemblées par triangulation, un peu comme les échafaudages, mais pour former des surfaces beaucoup plus complexes.
Explorons ces deux pistes, dans cet ordre.
Remarque préliminaire: pour ceux désireux d’approfondir le sujet l’équivalent anglais de cette expression est timber gridshell.
Si tout à l’heure vous vous êtes amusé avec un treillis de palissage, reprenez la petite arche que vous avez construite. Sinon vous pouvez vous contenter d’en former une avec une feuille de papier épais. Appuyez légèrement dessus. Le problème saute aux yeux: ça se déforme à la moindre sollicitation. Pas très engageant pour un principe structurel censé résister au vent et à la neige!
En fait la flexibilité des tiges qui a permis de courber le treillis se retrouve en partie dans le résultat final. Mais pourquoi dans ces conditions la yourte se révèle-t-elle si résistante? C’est que la déformabilité du mur est contenue par les poutres radiales du toit, qui agissent en quelque sorte comme des rayons rigides d’une roue, et par un cerclage au moyen de fortes sangles.
Donc si l’on veut réaliser un bâtiment tout en treillis, sans ajout de poutres ni autres renforts rigides, gage de légèreté et de cohérence, il faut faire en sorte que la résistance provienne de la forme elle-même. Comme on vient de le voir, ce n’est pas le cas d’une portion de cylindre formant voûte. Mais vous pouvez imaginer que si vous croisiez une première arche en treillis avec une autre identique placée perpendiculairement, vous obtiendriez une sorte de dôme qui serait beaucoup plus résistant. En reliant bien les deux treillis, la structure finale fonctionnerait comme une coque.
Il ne s’agit pas des coques de bateaux mais de coques architecturales réalisées à l’origine en béton. Rien à voir non plus, malgré une parenté morphologique, avec les dômes et autres voûtes en pierres des temps anciens. Question d’épaisseur. Une image suffira à s’en convaincre, celle de cette station-service de Deitingen en Suisse construite par Heinz Isler en 1968:

|
Heinz
Isler |
Le rapport portée/épaisseur est un critère intéressant pour évaluer l’efficacité d’une structure. Voici un petit comparatif (ce ne sont que des ordres de grandeur évidemment):
- poutre en bois: 20
- arche: 40
- coque en béton: 400 à 800
- membrane supportée par l’air: jusqu’à 300 000
Pour une construction en ‘dur’, les coques sont un excellent compromis entre la quantité de matériaux utilisés et la surface couverte. D’autant que les matériaux en question sont des plus banals, du béton pris sur une grille métallique.
L’exceptionnelle résistance d’une coque vient de sa forme, pas de sa masse. C’est le même principe que pour une coquille d’œuf. On peut voir une coque comme le développement d’une arche funiculaire de façon à générer une surface et non plus seulement une ligne.
La première réalisation de ce genre date des années 1920. Mais c’est surtout à partir des années 50 que le procédé se propage sous l’impulsion d’architectes comme Candela, Nervi, Esquillan. C’est à ce dernier que l’on doit la réalisation la plus monumentale, le CNIT de Paris-La Défense.
En plan, elle dessine un triangle équilatéral de 218 m de côté inscrit dans un cercle de 251 m de diamètre. C’est en quelque sorte un dôme tronqué de manière symétrique sur trois côtés et qui culmine à plus de 48 m. Compte tenu de ses exceptionnelles dimensions, la structure est faite de deux coques espacées d’environ 2 m et reliées par des cloisons. L’épaisseur totale varie en fait de 1,9 m au sommet à 2,7 m à la base, tandis que l’épaisseur de chaque coque varie de 60 à 120 mm. Les cloisons de liaison entre les deux font quant à elles 59 mm d’épaisseur.
Comme les coquilles d’œufs, de telles coques en béton se révèlent extrêmement solides malgré leur très faible épaisseur. Et comme les coquilles d’œufs, elles s’enfoncent assez facilement sous une charge ponctuelle un peu forte, ce qui conduit généralement à l’effondrement de tout le bâtiment.
Un autre inconvénient des coques est que la réalisation nécessite un moule. On peut parfois s’en passer, comme dans certaines constructions conçues par assemblages d’éléments préfabriqués, ou comme ces petits dômes où le béton est coulé sur un ballon que l’on gonfle. Mais ça reste un problème dès que la forme devient un peu plus complexe.
Le béton est quasiment le seul matériau utilisé. Je ne connais guère que les coupoles de télescopes faites dans une autre matière, la fibre de verre. Il faut dire qu’elle est beaucoup plus chère et difficile à travailler (il faut construire des moules et passer beaucoup de temps à empiler des couches successives de tissu de verre et à les enduire de résine après avoir patiemment attendu que la précédente ait séché).
La question qui se pose maintenant est de savoir si l’on peut réaliser une coque à partir d’un treillis. Si oui, les avantages seraient nombreux: grande économie de matière, pas besoin de moule, il suffirait de courber le treillis de manière adéquate, d’où facilité et rapidité de montage, critères qui sont aussi des dimensions de la légèreté.
L’idée de croiser deux treillis que j’ai suggérée plus haut n’est ni pratique ni économique. D’ailleurs si deux treillis à mailles carrées se croisent, l’on peut faire en sorte que les mailles se superposent à l’endroit du croisement. Cela veut dire que la même forme pourrait être obtenue avec un seul treillis.
La question devient donc: est-il possible de déformer un treillis simple en une surface à double courbure comme un dôme? Si vous avez toujours sous la main votre treillis de palissage, essayez, vous vous rendrez vite compte que c’est possible mais à condition de ne pas accentuer la courbure, sinon les lattes se disjoignent ou se rompent.
Il y a une raison géométrique à cette impossibilité de courber davantage le treillis: on ne peut pas plaquer un carré sur une sphère sans le déformer. Découpez un petit carré de papier et plaquez-le sur un bol ou une balle, vous constaterez qu’il ne colle pas à la surface à moins de faire des plis. Vous pouvez aussi réaliser un petit carré avec du fil de fer, c’est plus proche de la maille d’un treillis. En le plaquant sur une boule, vous pouvez cette fois lui faire épouser la surface mais au prix d’une déformation.
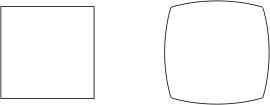
On pressent que si on laisse du jeu dans les connexions, l’ensemble du treillis devrait pouvoir se déformer plus amplement jusqu’à prendre la forme d’une coque. Tout le secret est là en effet: laisser du jeu.
Au final, le principe de construction d’une coque en treillis apparaît assez simple:
1. On commence comme pour le mur d’une yourte par assembler à plat sur le sol de longues lattes de bois selon un maillage généralement carré mais qui peut être aussi triangulaire ou hexagonal. On ne sert pas à fond les boulons ou les connecteurs situés à tous les points d’intersection pour permettre de légères torsions et de petits déplacements des lattes lors de la mise en forme.
2. Par une combinaison de poussées et de tractions, on déforme la trame plane en une surface à double courbure, qui peut être très complexe et ne pas se limiter à la calotte sphérique comme on le verra dans les exemples ci-après. Au cours du processus, et grâce au jeu qu’on a laissé, certains carrés s’agrandissent légèrement, d’autres rapetissent, beaucoup se déforment en losanges.
3. Une fois la forme finale désirée atteinte, on assure la jonction avec le sol et on sert bien tous les boulons. On obtient au bout du compte une structure extrêmement résistance par effet de coque. Pour accroître la rigidité, on peut ajouter des câbles diagonaux qui triangulent les carrés.
La première réalisation remarquable est l'œuvre de Frei Otto, un génie des structures légères que l'on retrouvera maintes fois dans cette étude. Pour être tout à fait exact, l'architecte était Carlfreid Mutschler, le bureau d'ingénierie Ove Arup & partners avec Ted Happold comme chef de projet, et Frei Otto était le concepteur de la forme-structure. Il avait déjà employé le procédé mais à échelle beaucoup plus modeste. Avec la Mannheim Multihalle construite en 1975 on passe dans une autre dimension: 7400 m² couverts, une longueur maximale de 160 m, une largeur maximale de 115 m, une portée maximale de 85 m, une hauteur maximale de 20 m pour un poids de seulement 14 kg/m². La structure est constituée d'un double réseau de longue lattes de bois de 5x5 cm et le tout est recouvert d'une membrane transparente en polyester.
Cette Multihalle de Mannheim était conçue au départ comme un bâtiment temporaire pour une exposition horticole. Plus de trente ans après elle est toujours debout. Comment expliquer alors que le procédé n’ait pas fait école? C’est que derrière la relative simplicité de la construction se cachent quelques grandes difficultés.
D’abord il n’est pas si facile de sélectionner du bois de qualité adéquate et de l’abouter en très longues lattes de plusieurs dizaines de mètres de long assez solides et assez flexibles pour prendre la courbure voulue sans se briser ni se fendre.
Ensuite la conception de la forme est extrêmement complexe dès que l’on s’éloigne un tant soit peu de la simple calotte. Et la Multihalle de Mannheim est en effet d’une grande complexité. De l’extérieur on dirait une succession de collines.

|
http://www.freiotto.com |
De l’intérieur on a une incroyable sensation d’espace (renforcée par la couverture transparente) et de fluidité avec des variations incessantes de courbure, d’inclinaison et de hauteur de la coque.

|
http://www.freiotto.com |
Pour concevoir cette forme, Frei Otto a procédé par étapes. Il a d’abord travaillé sur des maquettes au 1/100 constituées d’un réseau de câbles (un câble pour trois lattes) en exploitant l’idée d’une surface funiculaire qui par inversion donne une coque parfaite.

|
dans http://elib.uni-stuttgart.de/opus/volltexte/2001/761/pdf/wendland.pdf |
Après de nombreux tests et ajustements, notamment pour modifier les zones où des rayons de courbure trop faibles auraient entraîné la rupture des lattes, la maquette a servi de base à une modélisation numérique pour une étude plus poussée du comportement de la structure. À partir de là ont été calculés précisément la longueur de chaque latte et son positionnement. Une fois tout ce travail de conception accompli, le reste devenait simple et rapide: montage du treillis au sol, déformation, fixation. Encore fallait-il parvenir à franchir la première étape! À suivre ce résumé, on comprend qu’il ait fallu attendre 25 ans pour voir l’idée reprise pour une autre grande réalisation.
À Downland en Grande-Bretagne a été construit récemment un bâtiment original abritant le centre national d’études et de conservation des bâtiments traditionnels à ossature bois. Si le bâtiment en question se devait d’être en bois, les promoteurs ont choisi d’innover pour montrer le dynamisme de la filière. Au lieu d'une structure traditionnelle, ils ont opté pour la coque en treillis proposée par le cabinet de l'architecte Edward Cullinan avec l'assistance du cabinet d'ingénierie Buro Happold. La présence de ce dernier n'est pas un hasard puisqu'il a été fondé par Ted Happold, lequel a collaboré sur de nombreux projets avec Frei Otto, dont la Multihalle de Mannheim. Le résultat est une courbe continue qui dessine trois bulbes, une belle forme ondulante en harmonie avec les collines environnantes. Avec ses 48 m de long, ses 16 m de largeur maximale, et ses 11 m de hauteur, la structure pèse seulement 6 tonnes. Elle est constituée de 6000 m de lattes en chêne de 5x3,5 cm assemblées en un double réseau superposé à mailles carrées de 1 m qui au sol forme approximativement un rectangle de 30 m sur 52. La série de photos suivante montre bien les étapes de la construction:

|
|

|
|

|
http://www.burohappold.com |
Avec des rayons de courbure allant jusqu’à 6 m et des lattes mesurant jusqu’à 50 m, beaucoup d’efforts ont porté sur leur fabrication: sélection du bois, choix de la colle, conception des connecteurs pour éviter de faire des trous qui affaibliraient les lattes, etc.
De grands efforts ont été faits également pour modéliser le comportement de la structure. Car il fallait respecter les normes de construction en vigueur pour un bâtiment permanent destiné à accueillir du public.
Dans la foulée mais à l’opposé de ce projet ambitieux les britanniques nous ont gratifiés récemment d’une autre structure en coque à treillis de bois. Il s’agit cette fois d’une simple calotte posée sur une base hexagonale maçonnée de 9 m de diamètre. Elle a été conçue en 2002 par l’architecte Christopher Day pour un centre anthroposophique situé à Pishwanton. L’idée était de la réaliser en autoconstruction avec autant que faire se peut des matériaux locaux: lattes en mélèze (encore vert pour la flexibilité) de 3,5x2,5 cm de section et 3 m de long aboutées pour atteindre 12 m; treillis carré de 60 cm fait de deux couches de lattes; une coque consolidées par trois couches croisées de planches vissées pour que le bâtiment supporte le poids d’une toiture végétale.

|
|

|
images
David Tasker dans http://vs2.i-dat.org/fourthdoor/index.html |
Il y a à mes yeux une incohérence entre la réalisation de la coque selon un principe de légèreté et le résultat final renforcé de trois couches de planches pour supporter des tonnes de terre. Mais c’est leur problème et tout ce qui compte ici c’est de constater que le principe est utilisable en autoconstruction sans avoir recours à des modélisations poussées. À condition de savoir se contenter d’une simple calotte.
En guise de conclusion sur les réseaux en treillis, citons l'expérience originale de Shigeru Ban pour le pavillon japonais de l'exposition universelle de Hanovre. Il voulait une forme naturelle et une structure légère dont tous les éléments soient recyclables. Ayant déjà travaillé avec des tubes en carton, l'idée d'un réseau en treillis avec de tels tubes s'est vite imposée. Il s'est rapproché de Frei Otto et de Buro Happold qui l'ont aidé. La forme en trois bulbes ressemble un peu à celle de Downland. Elle fait 16 m de hauteur et couvre 3600 m². Elle n'a pu être conçue que par ordinateur. Le réseau consiste en 440 tubes en carton de 12 cm de diamètre et 40 m de long.
L'expérience consistant à employer du carton est originale mais encore limitée : d'une part par le fait qu'il a tout de même fallu recourir à des renforts en bois sinon la structure ne respectait pas les normes; d'autre part parce que tout a été démonté à la fin de l'exposition et qu'on ne peut donc rien tirer du comportement d'une telle structure sur une plus longue durée. Saluons toutefois l'esprit d'innovation.
L’autre direction prise par les assemblages non hiérarchisés conduit à préférer des éléments plus courts et rigides au lieu de longs et flexibles. L’idée cette fois est de concevoir des surfaces susceptibles d’être pavées par des triangles, avec pour avantages:
+ l’emploi de petits éléments quasi identiques (bambou, tubes d’acier, d’aluminium, etc.) facilitant la fabrication et le transport;
+ une structure facile à monter et à démonter si les connecteurs sont bien conçus, à l’instar d’un échafaudage,
+ avec du personnel peu ou pas qualifié.
L’idée de telles structures s’est progressivement élaborée autour de 1900. À la fin des années 30, plusieurs brevets ont été déposés pour des systèmes de connexion. Mais c’est surtout avec la construction des dômes géodésiques, culminant en 1967 avec la remarquable réalisation pour l’exposition universelle de Montréal, que ce principe structurel touche le grand public.
Bien que les premiers dômes géodésiques remontent aux années 1940, le monde les a véritablement découvert en 1967 à l’occasion de l’exposition universelle de Montréal.

Une énorme boule de plus de 80 mètres de diamètre donnant paradoxalement une impression de transparence et de légèreté. Une sorte d’OVNI venu se poser là en douceur. Une architecture de circonstance en cette ère triomphale où les hommes s’apprêtaient à poser le pied sur la Lune. Des américains pour être exact. Car ce dôme était le leur. À l’intérieur s’élevait un immeuble de six étages exposant ce que l’Amérique elle-même jugeait comme le summum de son inventivité: gadgets technologiques, œuvres d’art, jusqu’au programme spatial Apollo. Mais le meilleur témoignage de la réussite américaine était peut-être le dôme lui-même:
+ une boule correspondant aux 3/4 d’une sphère de plus de 80 mètres de diamètre, haute comme un immeuble de 20 étages;
+ 600 tonnes seulement;
+ une structure en deux couches espacées d’environ un mètre faite de tubes d’acier soudés de 9 cm de diamètre (il avait été prévu de les boulonner mais pour des raisons d’économie les tubes ont été soudés, rendant la structure indémontable);
+ une couverture de 1900 panneaux d’acrylique.
Succès assuré: 5,3 millions de visiteurs en 6 mois.
En 1976, à l’occasion de travaux de maintenance, un incendie s’est déclaré qui a détruit toute la couverture sans affecter la structure. Rebaptisée Biosphère, elle abrite aujourd’hui un centre d’information écologique.
Cette remarquable réalisation est due à Buckminster Fuller (1895-1983). On ne saurait le qualifier d’architecte à proprement parler. Sa démarche était beaucoup plus ambitieuse: embrasser le fonctionnement de l’univers, dévoiler les principes de régénération qui selon lui l’organisent et le réorganisent continuellement à toutes les échelles, et en tirer des application pratiques, notamment en architecture. Sa pensée est complexe, parfois un peu outrée, mais il a le mérite de l’avoir passée au crible de l’expérience. Cela n’a pas toujours réussi, mais ce qu’il en reste n’est pas moins remarquable. Relevons quelques unes de ses idées maîtresses sur lesquelles s’appuient ses réalisations.
Fuller a une approche véritablement cosmique dans la mesure où, pour lui, ce sont les mêmes principes qui gouvernent l’organisation de la matière à toutes les échelles, des atomes au système solaire en passant par les êtres vivants. Par conséquent une architecture sensée doit suivre les mêmes règles qu’il synthétise sous la dénomination synergetics pour synergetic-energetic geometry. Cela signifie d’une part que toute structure naturelle tend d’elle-même vers un état d’énergie minimale (principe bien connu en physique qu’il généralise), et d’autre part que son évolution se fait de manière synergique, c’est-à-dire que le comportement de l’ensemble n’est pas réductible à celui de ses éléments constitutifs (d’autres à la même époque employaient plutôt le vocable systémique). Tirant le fil de sa réflexion, il parvient à cette compréhension des jeux de force dans la matière:
“La compression est une ˝réalité centrale˝ ŕ laquelle on aime se référer, et cette réalité est considérée comme universellement étendue. On doit maintenant casser cette habitude et apprendre à jouer le jeu de la nature où la tension est première et explique la cohérence de l’ensemble. La compression est pratique, très pratique, mais toujours secondaire et discontinue." (cité dans http://www.redskyshelters.com/index.html, traduction personnelle)
Cette mise en avant de la tension le conduira, entre autres, à élaborer avec Kenneth Snelson le concept révolutionnaire de tenségrité (tensegrity en anglais pour tensional integrity) que l’on étudiera dans le chapitre suivant.
Ajoutons que Fuller avait avant l’heure une pensée que l’on qualifierait aujourd’hui d’environnementale. Il était parfaitement conscient du poids exagéré que fait peser l’homme sur la Nature. Donc conscient également du poids que l’architecture fait peser sur les ressources. De là une aspiration à des bâtiments plus légers, tout en étant autant sinon plus résistants que les ouvrages massifs grâce à la meilleure compréhension des principes structuraux permise par sa métaphysique. Dans ce domaine il s’est confronté avec succès à la matière. Preuve en est que les plus grands dômes construits avant l’ère moderne, St Pierre de Rome et le Panthéon de Paris, pèsent aux environs de 15 000 tonnes pour un diamètre de 50 mètres, tandis qu’un dôme géodésique de même diamètre construit par Fuller pèse mille fois moins!
Comme le suggère ce dernier exemple, le dôme géodésique se veut une application de ces conceptions à l’architecture. Cela ne s’est pas fait sans quelques essais et erreurs.
Mais pour bien comprendre de quoi il s’agit commençons par revenir sur la dénomination elle-même. En géométrie, on appelle géodésique d’une surface la ligne la plus courte qui, sur cette surface, joint deux points. On en a tous l’expérience sans avoir besoin de connaître la géométrie ni son vocabulaire. Par exemple chaque fois que l’on essaie de ficeler un paquet informe. Quand, après pas mal d’efforts, on croit être parvenu à un résultat satisfaisant et que l’envie nous prend de secouer un peu le paquet pour vérifier que tout tient bien, c’est la catastrophe, les ficelles semblent se détendre d’un coup. En fait elles ne se détendent pas, elles trouvent d’elles-mêmes leur vraie place, les chemins les plus courts, autrement dit les géodésiques.
Dans le cas d’une surface sphérique, les géodésiques sont tout simplement des ˝grands cercles˝, c’est-ŕ-dire que le trajet le plus court entre deux points quelconques A et B est l’arc de cercle qui a pour centre le centre de la sphère, pour rayon le rayon de la sphère, et qui passe par A et B:
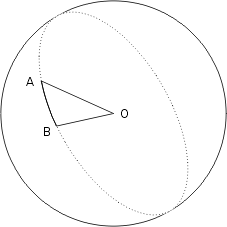
Fuller interprète les géodésiques comme des chemins d’énergie et de durée minimales. D’où l’idée de réaliser des sphères, qualifiées donc de géodésiques, à partir d’un certain nombre de tels grands cercles arrangés de manière qu’ils se croisent en formant des triangles. Si cette idée à l’air séduisante d’un strict point de vue géométrique, elle s’avère en pratique peu efficace. Problème de matériaux pour réaliser les cercles, mais surtout problèmes structuraux: les triangles que forment les géodésiques en se croisant et qui sont supposés donner sa tenue à la structure ont des dimensions fort inégales, d’où une mauvaise répartition des efforts.
Suite à ces premiers essais mitigés datant de la fin des années 40, Fuller a l’idée de revenir au triangle, plus précisément au triangle équilatéral qui constitue déjà une structure optimale. S’il est possible de réaliser une structure en assemblant uniquement de tels triangles identiques, on sera assuré de sa résistance grâce à une répartition régulière des efforts. Restant fixé sur la forme du dôme, sans doute parce que la sphère est également une forme optimale dans son système, la question devient: comment approcher au plus près la surface d’une sphère avec des triangles équilatéraux identiques? Le problème a été résolu il y a longtemps déjà, dès l’Antiquité en fait. Dans un espace euclidien tridimensionnel, il n’y a que trois polyèdres de ce genre qui s’inscrivent parfaitement dans une sphère:
1. le tétraèdre formé de 4 faces triangulaires équilatérales identiques, avec 4 sommets et 6 côtés:
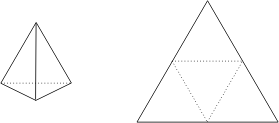
2. l’octaèdre formé de 8 faces triangulaires équilatérales identiques, avec 6 sommets et 12 côtés:
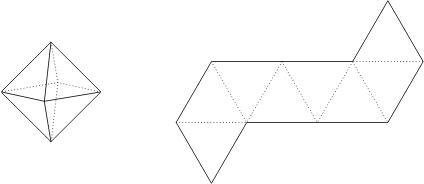
3. l’icosaèdre formé de 20 faces triangulaires équilatérales identiques, avec 12 sommets et 30 côtés:
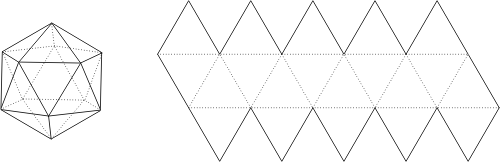
Ces figures appellent quelques remarques:
En remplaçant l’arc par la corde (ici le côté d’un triangle) pour dessiner la forme, on n’est plus à proprement parler sur une géodésique de la sphère. Mais pour Fuller l’essentiel est préservé dans la mesure où la corde étant plus courte que l’arc elle constitue en quelque sorte un raccourci encore plus économique. De là sans doute que l’appellation géodésique ait été préservée.
D’autre part, il est clair que plus le nombre de triangles augmente, plus la forme est proche de la sphère circonscrite. D’où l’idée d’augmenter encore leur nombre, à la fois pour coller au plus près de la sphère et pour augmenter la solidité en travaillant avec des éléments plus courts (rappelons que la résistance d’une tige au flambage est inversement proportionnelle au carré de sa longueur).
L’augmentation du nombre de triangles se fait en deux étapes.
Première étape: chaque triangle est subdivisé en triangles équilatéraux plus petits et identiques. C’est une des propriétés du triangle équilatéral de pouvoir se partitionner aussi facilement en figures similaires:

En divisant chaque côté en 2 parties égales par une ligne parallèle à un autre côté, on obtient 4 petits triangles équilatéraux identiques. On dit qu’on est à la fréquence 2. En le divisant en 3 avec deux lignes équidistantes et parallèles à un autre côté, on obtient 9 petits triangles équilatéraux identiques. On parle de fréquence 3. Et ainsi de suite, on obtient 16 triangles à la fréquence 4, 25 à la fréquence 5 etc.
On remarque que tous ces nouveaux triangles sont situés en-dehors de la sphère. D’où la seconde opération qui consiste à les ramener sur la sphère. La figure suivante montre le processus pour un triangle de fréquence 2:
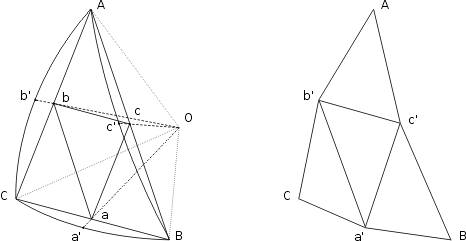
Voici le détail de la procédure:
1. le triangle équilatéral ABC est partitionné en 4 triangles équilatéraux identiques: Abc, aBc, abC et abc;
2. les points a, b et c sont ramenés sur la sphère, précisément: a se projette en a’ sur l’arc géodésique BC, b se projette en b’ sur l’arc géodésique AC, c se projette en c’ sur l’arc géodésique AB;
3. en fin de compte la structure se compose des triangles Ab’c’, a’Bc’, a’b’C et a’b’c’ dont tous les sommets se trouvent sur la sphère.
Ces opérations peuvent être effectuées sur n’importe lequel des polyèdres réguliers ci-dessus, le tétraèdre, l’octaèdre ou l’icosaèdre, et pour n’importe quelle fréquence. Le choix dépend notamment du type de dôme que l’on souhaite réaliser, en particulier du plan de coupe, car on ne construit jamais une sphère entière mais un hémisphère ou 3/8 de sphère ou 5/8 etc.
Pour un diamètre de sphère donné, on choisit la fréquence de manière à obtenir une longueur de tige appropriée. À titre d’exemple, la majorité des dômes géodésiques qui servent d’habitations et qui ont entre 5 et 10 mètres de diamètre emploient des tiges de 2 à 2,5 mètres de long et sont construits sur un icosaèdre de fréquence 3. Voici à quoi ressemble un tel dôme coupé à 5/8 de sphère:
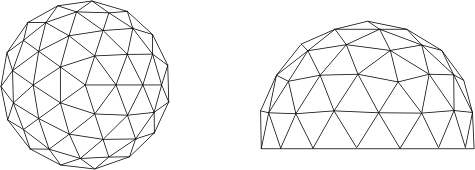
Il est important de remarquer que la seconde opération, celle par laquelle les sommets des nouveaux triangles sont ramenés sur la sphère, leur fait perdre leur équilatéralité. Du point de vue esthétique, cela ne fait guère de différence. Du point de vue des ouvriers qui fabriquent et assemblent les tiges, cela demande un peu d’attention.
Les calculs pour connaître le nombre et la longueur des différentes tiges ne sont pas très difficiles. D’ailleurs il existe des tables et même des petits logiciels de simulation qui donnent toutes les valeurs utiles en fonction du polyèdre de départ, de la fréquence, et de la position du plan de coupe. Voici à titre d’exemple les longueurs des tiges pour un dôme géodésique sur base d’icosaèdre de fréquence 2, en partant de R le rayon du cercle circonscrit:
1. longueur des arêtes Ab’, b’C, Ca’, a’B, Bc’ et c’A: 0,5465xR;
2. longueur des arêtes a’b’, b’c’ et c’a’: 0,6180xR;
Des milliers de dômes géodésiques ont été construits à ce jour, de toutes tailles et avec des matériaux divers. Pour les tiges: tubes d’acier, d’aluminium, de PVC, tiges en bambou, en bois de charpente, etc. Pour les connexions: soudures, connecteurs métalliques avec tiges boulonnées, connecteurs bois avec tiges boulonnées, clouées ou vissées, tiges attachées, etc. Bref, il y a autant de procédés constructifs que de constructeurs. Je ne rentrerai donc pas davantage dans les détails.
Retenons surtout que la conception d’une telle structure la rend extrêmement résistante, même avec des matériaux qui peuvent paraître de prime abord trop légers. Lorsqu’un effort s’exerce quelque part, il se diffuse partout par tension de certains éléments et compression d’autres, et ce faisant il se dilue, se disperse en quelque sorte. On ne compte plus les dômes construits dans le sud-est des États-Unis qui ont résisté à des ouragans.
Une remarque supplémentaire cependant.
On appelle angle axial l’angle que fait une tige avec le rayon:

On voit que pour une longueur de tige donnée, cet angle augmente avec le rayon (pour les amateurs: cosA=L/2R). Quand on conçoit une grande structure, vient le moment où cet angle est si proche de l’angle droit qu’elle perd toute résistance. La raison en est assez facile à comprendre.
Prenez trois tiges identiques (trois crayons, trois manches à balais, trois tubes PVC, etc.). Fixez-les solidement ensemble par une extrémité (plusieurs tours de ruban adhésif peuvent convenir). Reliez les autres extrémités par une ficelle.
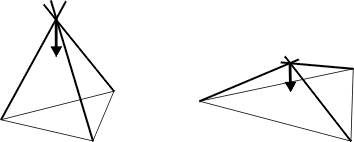
Premier essai (figure de gauche): ajustez la longueur de la corde de façon que, posée au sol, la structure forme quasiment un tétraèdre. Appuyez fortement sur le sommet: pas de doute, c’est du solide (on fait des petits tabourets de voyage comme ça). Deuxième essai (figure de droite): déroulez la corde pour rapprocher le sommet du sol. Appuyez une nouvelle fois sur le sommet. Vous constatez qu’une faible force suffit pour effondrer la structure (c’est pour la même raison qu’un parapluie ou un parasol se retourne si facilement).
Pour réaliser des dômes géodésiques de grand diamètre, l’idée consiste à construire deux structures parallèles et à les relier entre elles. Il y a plusieurs variantes dont voici la plus simple:
Les deux couches sont analogues et conçues selon les principes ci-dessus. Elles sont légèrement écartées l’une de l’autre, et légèrement décalées de sorte que le sommet d’un triangle appartenant à la première couche est en regard du centre d’un triangle appartenant à l’autre couche. Les deux couches sont reliées par un réseau tétraédrique c’est-à-dire que chaque sommet d’une couche est fixé par des tiges à trois sommets de l’autre couche.
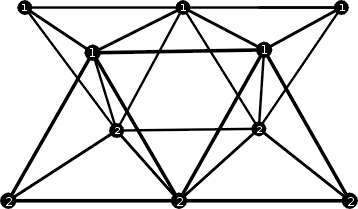
On voit en haut un fragment de la première couche (numérotée 1), en bas un fragment de la seconde couche (numérotée 2), et les liaisons entre les deux.
Voici une autre possibilité pour un dôme géodésique construit sur un double maillage hexagonal et non plus triangulaire. Plus précisément, la couche extérieure est hexagonale et la couche intérieure est formée d’hexagones et de triangles, ces derniers étant nécessaires pour rendre l’ensemble indéformable. Cette structure a l’avantage de donner une plus grande sensation d’ouverture même si elle est plus complexe à réaliser:
 |
Simon
Burt, Apex Photo Agency,
dans http://science.howstuffworks.com/eden3.htm |
Les dômes géodésiques sont devenus très populaires dans les années 70, surtout aux États-Unis et plus particulièrement dans les milieux dits de la contre-culture. Plusieurs raisons à cela:
+ ils constituent une alternative viable à la ˝maison carrée˝,
+ ils sont relativement faciles à réaliser en autoconstruction, du moins jusqu’à une dizaine de mètres de diamètre soit environ 70 m² au sol,
+ ils sont économiques à construire (certains sont même faits avec du bois de palettes) et économiques à l’entretien,
+ ils sont agréables à vivre, donnant à l’intérieur une belle sensation d’espace (à condition de ne pas s’acharner à le partitionner pour refaire dedans des pièces carrées).
Ce succès ne se dément pas puisqu’on trouve aujourd’hui rien qu’aux États-Unis une quarantaine de constructeurs officiellement répertoriés plus quelques uns au Canada, sans compter tous les auto-constructeurs. Un exemple de réalisation en bois:
 |
Soyons justes, le dôme géodésique n’a pas que des avantages, en particulier:
– si la structure est relativement facile à réaliser, la couverture pose plus de problèmes car il faut fermer des espaces triangulaires qui de surcroît forment entre eux des angles pas ordinaires: les fuites ne sont pas rares;
– difficile également de faire rentrer dans ces espaces triangulaires des portes et des fenêtres de formes rectangulaires conçues pour des maisons parallélépipédiques;
– impossible d’apporter des modifications, de faire des extensions, sauf à construire autre chose à côté;
– à de légères variations près, c’est toujours la même forme.
Cette forme de dôme est certes intéressante, son volume et sa rondeur étant plus attractifs que les boîtes parallélépipédiques. Mais si c’est pour remplacer toutes ces boîtes par de telles structures géodésiques, faire des villages, des villes entières de dômes, je ne vois pas l’intérêt. Le dôme n’a de sens que comme une forme possible parmi d’innombrables autres.
D’une part, les grandes réalisations comme le dôme de Montréal (toujours debout malgré un incendie) ou plus récemment l’Eden Project en Angleterre (qui sera détaillé dans la quatrième partie) prouvent la validité du concept d’assemblages non hiérarchisés. On dispose maintenant de suffisamment de recul pour être certain que, bien que très légères, ces structures sont extrêmement résistantes.
D’autre part, la réappropriation du concept par d’innombrables autoconstructeurs prouve qu’au niveau de monsieur et madame tout-le-monde aussi une alternative est possible aux principes constructifs traditionnels que sont les empilages et les assemblages hiérarchisés. Il est intéressant de remarquer que cela s’est fait tout seul, complètement en-dehors des circuits traditionnels de la construction, sans l’aide des architectes ni des maçons. Simplement par des gens aspirant à un nouvel art de vivre et qui osent franchir le pas, séduits par la forme, le procédé, et par la possibilité d’habiter autrement l’espace.
Nous avons vu deux manières de construire des structures non hiérarchisées, d’une part avec des tiges longues et flexibles aboutissant aux coques en treillis, d’autre part avec des tiges plus courtes et rigides aboutissant aux dômes géodésiques. Avons-nous fait le tour de la question? Peut-être pas. Il y a encore une piste à explorer, moins immédiate. Souvenons-nous de la possibilité de séparer dans une poutre la partie travaillant principalement en compression de celle travaillant exclusivement en tension. Eh bien l’idée serait d’étendre le procédé à l’ensemble de la structure et plus seulement à un élément. Cela aboutirait à relier les tiges entre elles par des câbles au lieu de les fixer ensemble à l’aide de connecteurs. Un niveau supplémentaire de simplification donc, du moins au niveau conceptuel.
Est-ce possible? Peut-on effectivement concevoir des structures qui seraient en quelque sorte réduites à leur plus simple expression: des tiges rigides tenues par un réseau de câbles tendus? Avantages: une grande économie de moyens et des matériaux employés à l’optimum de leurs possibilités. Notons que cela entraînerait la disparition des efforts de torsion particulièrement dommageables aux structures rigides, notamment au niveau des connexions, qu’elles soient d’ailleurs hiérarchisées ou non. Plutôt que nous plonger dans de savantes considérations théoriques, essayons plutôt de réaliser une telle structure.
Une seule tige ne permettant pas de faire grand chose sinon un piquet ou un mât démarrons d’emblée avec deux et voyons où cela nous mène.
Amusez-vous à manipuler deux crayons, vous comprendrez vite que la seule possibilité de faire une structure qui tienne est de les fixer en croix. Combien de manières de faire? Ou bien on les attache au point de croisement, ou bien on les relie par leurs extrémités avec quatre câbles.
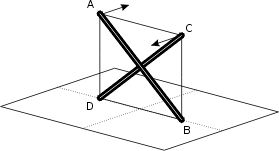
Remarquons que si l’on tend bien les câbles l’ensemble est géométriquement indéformable sans qu’il soit besoin de fixation supplémentaire à l’endroit où les deux tiges se croisent. C’est une structure complètement triangulée.
Voilà qui est déjà intéressant mais toute de même limité car au fond ce n’est qu’un rectangle que l’on a fabriqué. Une autre limite est l’apparition possible de déformations (si les câbles sont trop tendus par rapport à la flexibilité des tiges) qui font sortir du plan du fait que les tiges se croisent (flèches sur le schéma).
Voici peut-être un moyen de dépasser ces limites. Laissant B et D fixes et détendant les autres câbles, on fait pivoter A et C dans des directions opposées (ici A va vers l’avant et C part en arrière). Ainsi l’on sépare les deux tiges et du même coup on déploie la figure dans un espace à trois dimensions:
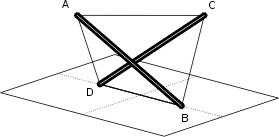
Le problème maintenant est que les tiges tombent si on ne les retient pas d’une manière ou d’une autre. Quels câbles ajouter pour qu’elles tiennent?
Faisons deux petites expériences en aparté pour essayer de comprendre ce qui se passe dans ce genre de situation où une tige est tenue pas un câble.
Première expérience:
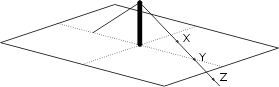
La tige est posée verticalement par terre (posée et pas plantée) et elle est maintenue droite par un câble. Une extrémité du câble est fixée au sol par un piquet. Question: où doit être fixée l’autre extrémité pour que ça tienne? En X au-dessus du sol, en Y au niveau du sol dans l’alignement du premier piquet et du pied de la tige, ou en Z au-dessous du niveau du sol? Réponse: X.
Deuxième expérience:
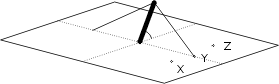
Dans cette variante la tige est inclinée latéralement par rapport à l’axe du câble. Même question: où faut-il fixer la seconde extrémité du câble pour que la tige ne tombe pas? En X du côté opposé à l’inclinaison, en Y sur l’axe, ou en Z du côté de l’inclinaison? Réponse: X.
Revenons à notre problème. En ajoutant deux câbles fixés au sol comme ceci, on arrive à la faire tenir:
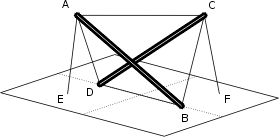
Maintenant imaginons que nous glissions une troisième tige entre les deux précédentes. Il doit être possible de faire tenir l’ensemble si: d’une part cette troisième tige est suffisamment longue pour que, une extrémité étant attachée en A et l’autre en C, cela ‘tire’ bien des deux côtés; d’autre part, on relie E et F à D et B à la fois pour tirer la tige vers le bas et pour remplacer la liaison DB:
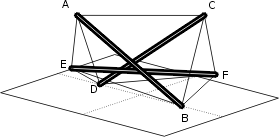
Concrètement:

Cet objet bizarre est appelé simplex. Bien que simple comme son nom l’indique, il est déjà intéressant. D’abord parce qu’il montre qu’il est effectivement possible de réaliser une structure tridimensionnelle faite d’éléments en compression qui ne se touchent pas enserrés par un réseau de câbles en tension.
Ceci étant, sa simplicité n’est qu’apparente car il n’est pas si facile à concevoir, on vient de le voir: une excellente capacité de visualisation dans l’espace ainsi qu’une bonne appréhension des forces en jeu sont exigées.
Il n’est pas non plus facile à réaliser: d’une part parce tant que tout n’est pas en place la structure ne tient pas (ce qui implique après coup que si un élément lâche, tout lâche: coupez un câble et voyez ce qui se passe…); d’autre part parce qu’il n’est pas aisé de fixer tous ces câbles tout en ajustant à la fois leur longueur et leur tension pour que chaque tige soit précisément positionnée. Et encore n’avons-nous ici que 3 tiges et 9 câbles, imaginez ce que ça doit être quand on augmente leur nombre!
Remarquons encore:
+ c’est quasi magique, la structure prend forme en fixant le dernier câble; ce qui n’était qu’un tas de tiges et un embrouillamini de câbles devient subitement une structure tridimensionnelle: étonnant!
+ c’est quasi magique, la structure tient toute seule alors que les tiges ne se touchent pas, qu’elles semblent flotter dans l’air: fascinant!
+ la structure acquiert sa rigidité en tendant bien les câbles; s’il n’y a pas suffisamment de tension, elle se déforme à la première sollicitation voire sous son propre poids; c’est comme si elle était d’autant plus solide qu’elle emmagasinait plus de force (dans les limites permises par la résistance des matériaux évidemment);
+ ici, chaque extrémité est reliée à trois autres, ce qui fait en tout neuf câbles; il aurait été possible d’en mettre plus, jusqu’à douze; une telle redondance pourrait s’avérer utile dans certains cas; mais elle n’est pas si facile à réaliser; le problème est que, du fait que la structure n’est plus optimale, une surtension dans un câble n’est pas forcément transmise à tous les autres; peuvent se produire des comportements inattendus comme des relâchements ici ou là.
Je vous encourage à faire vos propres expériences avec le simplex pour mieux appréhender comment marche une telle structure. Les structures plus complexes ne sont guère que des variations de celle-ci.
Les spécialistes se disputent la paternité de ce principe structurel. Citons:
- les structures tendues et autotendantes ou les réseaux autotendants de George Emmerich (1925-1996),
- les sculptures en floating compression de Kenneth Snelson (1927-),
- la tensegrity de Buckminster Fuller (1895-1983), contraction de tensional integrity.
Tout ça date à peu près de la même époque, autour de 1950, et correspond à peu près à la même chose. Finalement c’est le terme tensegrity qui a prévalu, francisé en tenségrité pour tension et intégrité.
Esquissons une définition, inspirée de René Motro, directeur du laboratoire de génie civil de Montpellier et spécialiste de la tenségrité: système stable autoportant, constitué d’un ensemble discontinu d’éléments en compression à l’intérieur d’un réseau continu d’éléments en tension. Développons:
système
Une structure en tenségrité est un système dans la mesure où le comportement de l’ensemble n’est pas réductible aux comportements de ses seuls éléments. C’est le propre en fait de toute structure non hiérarchisée. Cela signifie entre autres que connaître la résistance des éléments ne permet pas de connaître de manière immédiate la résistance de la structure (d’où des problèmes lors de la conception). Dans une structure hiérarchisée au contraire, la connaissance de la résistance des poutres primaires suffit pour connaître la résistance de l’ensemble du bâtiment.
stable
La structure est stable dans la mesure où elle retrouve son équilibre après une perturbation. Prenez un Simplex et appuyez dessus. Il se déforme par élasticité des câbles. Relâchez l’effort, il reprend sa forme.
Notons en passant que la structure absorbe les efforts en se déformant (l’ampleur de la déformation étant inversement proportionnelle à la tension régnant initialement dans le réseau de câbles et proportionnelle à l’élasticité du matériau dont sont faits les câbles). D’où certaines difficultés s’il faut la fermer. Il faut recourir à une couverture susceptible elle aussi de se déformer dans les mêmes proportions, soit sous forme d’une membrane élastique, soit sous forme de petits panneaux rigides assemblés en écailles pour rester mobiles les uns par rapport aux autres.
autoportant
Cela signifie que la structure tient toute seule, que sa forme et son intégrité ne dépendent ni de sa liaison avec le sol (pas besoin de points d’appuis au sol pour dessiner la forme) ni de la gravité (la structure peut sans déformations être soulevée, retournée, déplacée…). Elle garde d’ailleurs la même forme en apesanteur. D’où son intérêt pour des structures spatiales, surtout combiné au fait que certaines peuvent être rendues déployables (il suffit de réaliser une structure prémontée avec les câbles complètement détendus et de prévoir un système qui les raccourcit jusqu’à la longueur adéquat puis les met en tension).
séparation tension-compression
Les efforts de compression sont entièrement localisés dans des éléments disjoints les uns des autres. Ceux-ci sont reliés par un réseau continu d’éléments en tension. De ce fait, toute modification locale de tension est immédiatement répercutée dans tout le réseau. Ceci est compensé par un accroissement de compression dans certaines tiges. C’est ainsi que la structure réagit globalement aux efforts. Cela la rend particulièrement résistante. En contrepartie il est très difficile de prévoir précisément son comportement. Il y a aussi l’inconvénient que la rupture d’un élément a forcément des répercussions sur l’ensemble. Mais notons à ce propos: 1. on sait faire aujourd’hui des éléments extrêmement résistants à la tension; 2. les éléments subissant la compression sont courts, donc les risques de flambage réduits; 3. il est possible d’introduire un certain degré de redondance, même si ce n’est pas facile à calculer.
Insistons à nouveau sur l’énorme différence de comportement entre structures hiérarchisées et non hiérarchisées. Les premières sont conçues pour canaliser progressivement vers le sol les efforts à travers des éléments de plus en plus résistants qui reçoivent de nombreux ruisselets de forces en provenance des niveaux hiérarchiques supérieurs. Tandis que dans les secondes, les forces sont dispersées comme dans un réseau dense de capillaires, pour finir en partie absorbées de manière élastique et en partie évacuées dans le sol.
intérieur en compression dans une gaine en tension
Les petites expériences réalisées plus haut permettent de comprendre que la structure ne tient que si tous les éléments en compression sont situés à l’intérieur d’une enveloppe d’éléments en tension. C’est cette enveloppe qui délimite la forme. S’il s’agit d’un bâtiment qui demande à être fermé, c’est sur cette enveloppe que prendra appui la couverture. Et comme elle a une certaine élasticité, on retrouve la nécessité d’une couverture capable de se déformer également.
Si l’on sait réaliser un élément tel que le Simplex, on se doute qu’il est possible de concevoir des formes beaucoup plus complexes. Par exemple cette figure dérivée du tétraèdre:
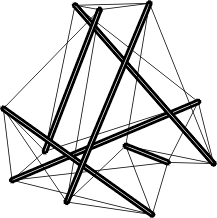
C’est une bien jolie forme dira-t-on mais est-il réellement possible de se servir d’un tel principe structural pour construire des bâtiments? C’était l’ambition avouée de Fuller. Il faut reconnaître que ses tentatives n’ont hélas pas abouti. Il aurait voulu en particulier faire des dômes géodésiques en tenségrité. Ses échecs l’ont contraint à se rabattre sur des dômes réalisés uniquement avec des tiges rigides. Mais cela ne l’a pas empêché de continuer à croire en la validité du concept et à poursuivre toute sa vie des recherches dans cette direction.
Au contraire de Snelson, co-inventeur du concept, qui a préféré se cantonner au domaine de l’art:
"Je suis persuadé sur la base de ma longue expérience dans la construction de structures en tenségrité de toutes formes et toutes tailles que le principe en lui-même est inapplicable à la construction de bâtiments. De nombreux architectes et ingénieurs ont travaillé dans ce sens et continuent de le faire. Cela fait cinquante ans. Aucun n’a prouvé que l’emploi de ce principe structurel avait le moindre intérêt dans ce domaine." (cité dans http://www.alumnos.unican.es/uc1279/6-Applications.pdf, traduction personnelle)
Cette division perdure. À leur tour les chercheurs d’aujourd’hui se partagent entre ceux qui ne voient dans la tenségrité que des idées inspirantes, susceptibles d’applications pratiques à condition d’être notablement adaptées, et ceux qui croient possible d’appliquer les principes tels quels. Sans rentrer dans la dispute, voyons ce qu’on arrive déjà à faire.
mâts, tours, arches
On doit à Snelson un certain nombre de tours (dont une de plus de 30 mètres de haut), arches et autres formes intermédiaires spectaculaires qui tiennent davantage de la sculpture que de l’architecture.
 |
|
 |
Lorsque les câbles se confondent avec l’arrière-plan, on a vraiment la sensation d’une structure flottante, expression chère à Snelson, ou carrément d’éléments en lévitation. Fascinant mais guère utilisable pour faire des maisons.
dômes
Reprenant les projets de Fuller, Robert Burkhardt a conçu à la fin des années 90 un dôme en tenségrité.
 |
Robert
Burkhardt
http://www.channel1.com/users/bobwb/index.html |
Le premier modèle de ce genre possède les caractéristiques suivantes:
- 5,28 m de diamètre extérieur pour 4,06 m de diamètre intérieur;
- 102 tiges de bois de 2,54 cm de section et 1,22 m de long;
- 570 câbles en nylon.
Ce dôme s’avère aussi solide et léger qu’un dôme géodésique traditionnel, plus compliqué à monter, mais plus simple dans ses constituants puisque toutes les tiges sont identiques et qu’on se passe de connecteurs. En revanche il semble difficile à couvrir et peu pratique en guise d’habitation.
réseau bidimensionnel
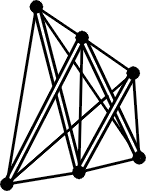
Des recherches effectuées au laboratoire de génie civil de Montpellier sous l’égide de René Motro ont abouti à la conception d’un module de base appelé V-expander qui, répliqué un grand nombre de fois, permet de réaliser de grandes surfaces n’ayant pas plus d’épaisseur que celle du module:
 |
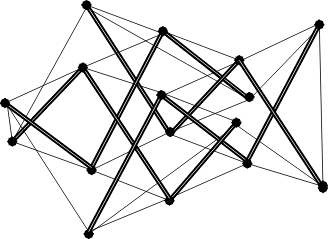 |
En 2000 a été réalisé selon ce principe une surface portante de 82 m² pour un poids de seulement 900 kg, capable de supporter environ 160 kg/m² soit au total près de 13 tonnes.
Les principaux avantages des structures en tenségrité sont: légèreté, stabilité, résistance. Quant aux inconvénients: difficulté de conception, de construction, de couverture des surfaces.
Que pour le moment les inconvénients l’emportent largement sur les avantages et que les réalisations soient très en retrait par rapport aux ambitions n’empêchent pas de considérer avec intérêt ces structures. La raison principale en est bien sûr qu’elle vont droit au cœur du principe structurel tension/compression. Nous voilà parvenus très loin des structures conventionnelles stabilisées par leur poids via des éléments comprimés, loin aussi des assemblages rigides. Cela prouve au moins qu’il est possible d’envisager les structures d’une manière radicalement nouvelle, que c’est donc un domaine largement ouvert à la recherche et à la créativité.
Quant au futur de la tenségrité, on peut l’envisager dans deux directions, toujours les mêmes.
Poursuivre les recherches dans la pure tenségrité. À force, finiront bien par émerger des géométries et des matériaux susceptibles de réelles application pratiques. Mais il ne semble pas que ce soit pour un futur immédiat, du moins pour le grand public (probablement plus tôt pour des applications spatiales).
Ou bien s’inspirer seulement de certains principes de la tenségrité sans souscrire totalement au dogme pour réaliser dès à présent des structures opérationnelles. Par exemple le câble-dôme de David Geiger ou les dômes de Shelter Systems dans lesquels les éléments en tension ne sont plus des câbles mais des membranes. C’est pourquoi ces exemples seront détaillés dans la partie suivante consacrée justement aux architectures à membranes.