|
|
Bien que disponible gratuitement pour que tout le monde y ait accès sans barrière, ce document n'est pas pour autant sans valeur. Vous pouvez participer aux frais de création et de diffusion, en vous rendant à la page contact.
Avec les assemblages non hiérarchisés on a franchi une étape importante par rapport aux assemblages hiérarchisés dans la mesure où forme et structure sont devenus indissociables. Mais les uns comme les autres se heurtent à la difficulté de devoir recouvrir après-coup la structure. Difficulté d'autant plus grande que l'on n'a plus affaire à de très classiques rectangles mais à des triangles et autres polygones accolés selon des angles inhabituels, voire à des formes tarabiscotées conçues même parfois pour se déformer élastiquement. Remarquons en passant qu'après l'incendie qui l'a détruite, la couverture du dôme de Montréal n'a pas été remplacée. C'est maintenant une structure ouverte, le centre écologique prenant place dans un bâtiment ordinaire construit à l'intérieur du dôme.
Un pas supplémentaire vers la simplification serait de construire avec une membrane qui assurerait toutes les fonctions: structurelle, délimitation de la forme et couverture de protection. Essayons pour voir.
Il fait beau, quelqu'un suggère de manger dehors. Sauf que quelques délicats, trouvant le Soleil un peu fort pour leur peau et leurs yeux sensibles, réclament une protection. Comme il n'y a pas de parasol, il faut faire avec une simple bâche. Attachée aux quatre coins à hauteur convenable cela fournit une protection satisfaisante. Tout le monde est content. Jusqu'à ce que survienne un petit coup de vent qui ballotte tant et tant la membrane que l'on craint qu'elle ne se déchire. La solution est vite trouvée: tendre davantage les liens de fixation. Miracle, l'ampleur des oscillations s'atténue aussitôt. Mais voici que se produit une nouvelle alerte, une averse, oh pas très forte, suffisante tout de même pour qu'en quelques minutes une poche d'eau se forme. Pas d'autre solution que de pousser par dessous avec un balai pour vider l'eau.
Pas si facile en fin de compte de construire avec une membrane. L'on sait seulement qu'elle n'a aucune tenue et que pour lui donner à la fois une forme appropriée et lui conférer une aptitude à résister à des forces extérieures il faut la tendre fortement entre des supports. Ceux-ci doivent être suffisamment rigides pour ne pas se plier sous l'effort. Une véritable architecture à membrane est nécessairement une structure tendue. Sinon on en revient à une membrane qui n'est qu'un élément de couverture venant remplir l'espace entre les tiges ou les câbles d'un assemblage.
L'idée des architectures à membranes évoque irrésistiblement la tente. Après la grotte et parallèlement à la hutte faite de branches entrecroisées c'est probablement la plus ancienne forme d'habitat humain. Une peau attachée entre deux arbres, voilà déjà un abri, déjà un embryon de tente. Au fil des perfectionnements, on en est arrivé à des constructions plus élaborées qui assurent une protection correcte (selon les cas au Soleil, à la pluie, au vent, au froid) et offrent un espace de vie suffisant pour une famille. Bref, les tentes traditionnelles s'avèrent plutôt confortables dans leurs contextes géographiques et climatiques respectifs, tout en étant relativement faciles à fabriquer (facile mais long, la membrane en particulier réclame pas mal de travail, moins tout de même que tailler des poutres ou des pierres), à entretenir (fréquemment), à monter et à démonter. Fortes de ces avantages, c'est à se demander pourquoi elles restent l'apanage de peuples nomades, pourquoi les hommes en se sédentarisant les ont abandonnées au profit de maisons en durs. On le comprendra par la suite.
Selon le climat, les matériaux disponibles, les modes de vie, différents modèles de tentes ont été inventés. Parmi les plus intéressants, citons:
- le tipi des indiens des plaines américaines

- la yourte mongole, qui s'étend en fait jusqu'au Tibet
 |
- la tente noire des gens du désert, que l'on retrouve du Maghreb au Tibet
 |
De ces trois modèles, seul le dernier correspond véritablement à une architecture à membrane car il y a interdépendance entre celle-ci, les mâts et les câbles. Dans la yourte, on l'a vu dans la deuxième partie, la couverture de feutre n'a pas de fonction structurale, elle est simplement posée sur une structure en bois indépendante. Idem pour le tipi qui consiste en un simple cône fait de longues perches de bois que viennent recouvrir des peaux de bison.
Probablement originaire de Mésopotamie, la tente noire a envahi une longue et mince bande de l'Atlantique au Tibet. Elle tient son nom de la couleur des chèvres dont les poils servent à réaliser la couverture (certains ajoutent un peu de laine de mouton, et les tibétains quant à eux utilisent des poils de yaks). Les fibres sont filées puis tissées grossièrement en une longue bande d'une dizaine de mètres de longueur et d'une trentaine de centimètres de largeur. Plusieurs bandes semblables sont cousues côte à côte pour former un grand rectangle, et un ou deux de ces rectangles servent à couvrir une tente.
Un certain nombre de perches servent quant à elles de mâts de soutien. Deux ou trois supportent la partie centrale sommitale, d'autres les angles. Elles sont reliées par un réseau de cordes et fixées au sol par de long haubans qui assurent un ancrage solide.
Une fois posée sur l'ossature, le poids important de la couverture (tellement qu'il faut un, voire deux, robustes animaux pour la transporter: chameaux, dromadaires ou yaks) met en tension les câbles. La tente prend alors sa forme définitive et acquiert sa résistance par le jeu réciproque entre le poids de la membrane, la tension des câbles, et la compression des mâts. Par conséquent, bien qu'elle ne soit pas elle-même en tension, la membrane est bien ici un élément de structure autant qu'un élément de forme et de protection, contrairement à ce qui se passe dans un tipi ou une yourte.
Les tentes noires traditionnelles occupent un carré de 5 à 10 mètres de côté pour une hauteur maximale de 2 à 2,5 mètres, assez faible pour conférer un profil aérodynamique.
Le tissage est intentionnellement lâche pour laisser circuler l'air et permettre aussi l'évacuation de la fumée. En cas de pluie, les fibres gonflent en absorbant l'eau, ce qui referme les pores et procure une certaine étanchéité (à condition que l'averse ne dure pas trop longtemps! cette tente est plus appropriée aux régions arides qu'aux régions pluvieuses).
Même si le bois servant à faire les mâts est rare, l'élément le plus critique de cette structure est bien évidemment la membrane. Sa durée de vie est relativement courte, guère plus de 5 ans, et elle nécessite de fréquentes réparations. Voilà probablement qui explique qu'elle n'ait pas survécu à la sédentarisation, surtout lorsqu'il y a besoin de couvrir des surfaces importantes telles que granges à foin, greniers à grains, etc., bien protégées autant des intempéries que des rongeurs.
Autre précurseur des architectures à membranes, la marine à voile. Les mâts et leurs haubans, les voiles et leurs gréements constituent tous ensemble de véritables structures tendues. On imagine qu'il suffirait de pas grand chose pour transformer cette architecture navale en architecture terrestre, un simple basculement de la voile de la position verticale à la position horizontale. À ma connaissance seuls les romains s'y sont essayés. Leurs arènes et théâtres étaient fréquemment pourvus de toits de toile rétractables directement inspirés de la marine à voile: mâts de soutien, câbles de maintien et de manœuvre, grandes toiles disposées horizontalement pour former des dais, le tout manœuvré par d'anciens marins. De là le nom de velum, voile en latin, donné en français à ces toits de toile.
Cette entorse à leur goût du robuste et du massif ne vient pas d'un désir d'ouvrir leurs amphithéâtres mais plutôt de leur incapacité à couvrir d'aussi vastes espaces avec des toits en dur. Cela explique sans doute qu'ils n'aient pas poursuivi la transposition à l'architecture des techniques de construction navale.
Si vous aviez à concevoir une maison avec une membrane souple jouant un rôle structural, comment vous y prendriez-vous? Pas facile en vérité, surtout s'il s'agit d'un habitat permanent et pas seulement d'une tente de camping.
Pas facile de parvenir à équilibrer tensions, compressions, et forces extérieures changeantes. Quel campeur n'a pas vu une tente s'effondrer, s'envoler ou se déchirer? Quel marin n'a pas vu une voile se déchirer, un mât ou un hauban se casser, un navire chavirer par mer calme lors d'un simple changement de cap? La difficulté augmente évidemment avec la dimension de l'ouvrage (disons de 40 à 200 m² pour une habitation à comparer avec les quelques mètres carrés d'une tente de camping).
Pas facile non plus de modeler une forme de dimensions respectables qui n'accumule pas des tonnes de neiges ou d'eau. Cf. les poches d'eau qui se forment fréquemment sur les toits des tentes de camping ou des auvents en toile. Dans des conditions de vacances ou de transhumance on se dit que ce n'est qu'un mauvais moment à passer. Pour un habitat permanent, c'est beaucoup moins acceptable.
Pas facile encore de trouver une membrane adéquate, à la fois résistante à la tension et durable. Les matériaux traditionnels tels que la laine et le coton s'avèrent bien peu performants. On a tous le souvenir de ces vieilles tentes en toile de coton qui s'avachissent et dégouttent à la première averse, qui moisissent quand elles ne sèchent pas immédiatement, qui se décolorent et cuisent au Soleil, pour finir par se déchirer au prochain coup de vent.
Tout bien considéré, les voiliers et les tentes ne sont pas tant des modèles pour les architectures à membrane modernes que des retardateurs de cette révolution. Car il a fallu attendre longtemps pour qu'elle se produise. Le tournant se situe à la fin de la seconde guerre mondiale. Il importe cependant de remarquer que ce tournant n'est pas le produit de quelque avancée technique mais qu'il est d'abord conceptuel.
D'un part, la conception des premières formes complexes et l'évaluation des forces en jeu se sont faites sans recourir à des modélisations mathématiques ni à des machines à calculer. Frei Otto s'est inspiré de modèles physiques tels que bulles de savon ou poids suspendus à des réseaux de câbles.
D'autre part, les premières grandes réalisations datent d'une époque où des membranes performantes n'existaient pas encore. Pour le pavillon allemand de l'exposition universelle de Montréal en 1967, Frei Otto s'est servi en guise de substitut de membrane d'un réseau de câbles d'acier recouvert d'un gigantesque filet d'acier (diamètre des brins 12 mm, taille des mailles 50 cm) recouvert à son tour d'une membrane translucide, le tout faisant plus de 8000 m² et étant supporté par 8 mâts culminant à 38 m.
J'insiste, cette révolution est avant tout celle du sens. Les tentes nomades et les expériences des romains n'ont pas pu se prolonger en-dehors de leurs contextes car elles n'avaient plus de sens. Idem pour la tente de campement (des armées avant d'être de camping) dont le seul prolongement a été la grande tente de cirque au 19e siècle pour laquelle la mobilité primait sur la durabilité et le confort. Les modernes architectures à membrane ne sont pas nées des nécessités d'un mode de vie particulier (mobilité) ni d'avancées techniques (nouveaux matériaux) mais d'une nouvelle aspiration:
"Nous construisons trop. Nous gaspillons l'espace, la terre, la matière, l'énergie. Nous continuons à construire des bâtiments non naturels comme aux temps passées. Notre époque demande plus de légèreté, d'économies d'énergie, de mobilité, d'adaptabilité, en un mot des constructions plus naturelles, sans négliger les besoins de protection et de sécurité." (Frei Otto cité dans http://www.redskyshelters.com/index.html, traduction personnelle)
Frei Otto (1925-) est justement la personne qui a le plus contribué à cette révolution. Porté par cet élan de créer une nouvelle architecture, il a étudié les tentes traditionnelles, les voiliers, les ballons, les cerfs-volants, les avions; il a étudié les squelettes des vertébrés, les toiles d'araignée, les plantes, les bulles de savon; il a réalisé d'innombrables expériences, maquettes, modèles; il a synthétisé tout ça dans de nombreuses réalisations architecturales remarquables qui vont des coques en treillis aux structures pneumatiques en passant par des structures à câbles tendus et à membranes tendues, sans oublier quelques ponts. Citons:
- en 1955 un kiosque à musique à Kassel qui semble aussi léger et aérien qu'un papillon;
- en 1967 le pavillon allemand (Allemagne de l'Ouest à l'époque) de l'exposition universelle de Montréal (conçu avec Rolf Gutbrod), à comparer avec le dôme géodésique construit par Fuller pour les USA pour le même événement;
- en 1972, inspiré du précédent, le toit du stade olympique de Munich, un réseau de câbles recouvert d'un filet à mailles de 75 cm recouvert à son tour de panneaux en plexiglas, l'ensemble couvrant plus de 35 000 m² et supporté par 8 mâts culminant à 76 m (avec Heinz Isler Günter Behnisch et Jurgen Joedicke); ce n'est qu'un élément d'un gigantesque ensemble construit selon le même principe qui couvre au total près de 75 000 m², la plus grande structure permanente du genre, et comprenant en plus du stade la salle de gymnastique et la piscine;
- en 1975-1980 la salle de sport de l'université Abdul Aziz de Jeddah (Arabie Saoudite);
- en 2000 le pavillon japonais pour l'exposition universelle de Hanovre (avec Shigeru Ban)...
Ajoutons qu'il a fondé en 1960 l'institut des structures légères affilié à l'université de Stuttgart (Institut für Leichtbau Entwerfen und Konstruieren, http://www.uni-stuttgart.de/ilek/ ).
Autres personnages marquants: Walter Bird, David Geiger (1935-1989) et Horst Berger (1928-). Ils ont tous trois travaillé chez Birdair, firme fondée par le premier en 1956 et spécialisée à l'origine dans les structures pneumatiques (voir chapitre suivant), puis les deux derniers ont fondé Geiger Berger Associates en 1968, spécialisée dans l'intégration des structures tendues dans des bâtiments permanents. Entre autres réalisations citons:
- en 1981 le Haj Terminal de Jeddah, 210 dais de forme conique constitués d'une simple membrane, couvrant en tout plus de 40 hectares et capable d'abriter 100 000 pèlerins du Soleil du désert;
- en 1994 le grand hall de l'aéroport international de Denver; dans cette ville habituée à des coup de vent violents et à de fortes chutes de neige, cette réalisation a achevé de convaincre les professionnels et le grand public que de telles architectures ne sont pas que de jolis abris pour expositions temporaires (même si le toit a été partiellement et temporairement endommagé par une violente tempête en 2003).
La grande contribution de Berger a été de trouver en 1974 comment modéliser mathématiquement la forme d'une structure tendue. Jusqu'alors il fallait se contenter de modèles approximatifs réalisés notamment avec des films de savon. C'est ce qui a permis une explosion de formes jamais vues en architecture et des réalisations monumentales qui ont passé avec succès l'épreuve du temps et des éléments. Mais on rentre là dans de la cuisine technique, la vraie révolution, celle du sens, l'ayant précédée.
 |
Frei
Otto, kiosque
http://www.freiotto.com |
 |
Frei
otto, complexe olympique de Munich, 1972
http://fr.wikipedia.org/wiki/Image:Olympiastadion_1.jpg |
 |
Horst
Berger, Tennessee Pavilion, 1979
galerie photos des structures tendues du NJIT http://www-ec.njit.edu/civil/fabric |
 |
laboratoire
de recherches M & G de Venafro, Italie
réalisation Samyn and Partners, photo Matteo Piazza |
 |
Horst
Berger, King Fahd Stadium de Riyad, Arabie Saoudite, 1985
galerie photos des structures tendues du NJIT http://www-ec.njit.edu/civil/fabric |
 |
réalisation
Birdair
http://www.birdair.com |
C'est bien évidemment l'élément le plus important qui donne forme, résistance et protection au bâtiment. Il lui est demandé énormément:
- supporter la pré-tension à laquelle elle est soumise en permanence;
- supporter des surtensions temporaires souvent bien plus considérables, celles dues au vent notamment;
- ne pas se détendre ni se dégrader sous l'effet de l'humidité, de la chaleur ou des ultraviolets;
- si nécessaire être étanche à l'eau, à l'air, résister au feu, etc.
Lourd cahier des charges! Tellement qu'avant les années 70 il fallait la plupart du temps se contenter de matériaux inappropriés tels que les toiles de coton, ou bien recourir à un réseau de câbles comblé dans un second temps avec des membranes sans fonction structurale. Ces temps sont révolus, l'on dispose aujourd'hui de matériaux performants et durables.
Les principaux matériaux utilisés en guise de membranes dans les structures tendues sont des composites constitués:
- d'un support en fibres synthétiques tissées qui procure à la membrane la résistance mécanique à la tension,
- d'une enduction en polymère qui assure l'étanchéité, la protection et permet de réaliser des soudures entre lés.
L'industrie chimique fournit quantités de fibres et d'enduits polymères. Parmi les innombrables combinaisons possibles, seules deux s'approchent suffisamment du cahier des charges idéal pour être couramment employées en architecture en guise de membranes dans les structures tendues: le tissu de fibres polyester enduit de PVC et le tissu de fibres de verre enduit de polytétrafluoroéthylène, PTFE en abrégé.
Le polyester est une fibre facile à fabriquer et à travailler, peu coûteuse, mais néanmoins très résistante à la tension. Elle possède également une bonne élasticité, ce qui autorise de légères imprécisions lors du montage. L'inconvénient est qu'elle est sensible au vieillissement, c'est-à-dire que l'âge tend à affecter ses propriétés.
Le PVC ou polyvinyle chlorure est un matériau aussi commun, facile à travailler et bon marché que le polyester. On le trouve d'ailleurs dans de nombreux produits d'usages courants: tuyaux et canalisations, matelas et jouets gonflables, liners de piscines, bâches d'étanchéité pour les travaux publics, etc. Divers additifs lui confère souplesse, résistance aux UV, au feu, à la décoloration, aux moisissures, etc. Il a l'inconvénient de dégazer des substances pas franchement bonnes pour la santé.
Ces deux matériaux se complètent bien. Selon leur qualité, la durée de vie de la membrane peut atteindre 10 à 15 ans.
Le tissu de verre (à ne pas confondre avec la laine de verre employée comme isolant ni avec la toile de verre utilisée pour tapisser les murs même si tous sont réalisés avec du verre) possède également une excellente résistance à la tension. Mais il est moins élastique que le polyester et même un peu cassant, ce qui oblige à une grande précision et une grande délicatesse lors de la réalisation de la membrane et son installation. Il possède en revanche un grand avantage: il n'est pas affecté par le vieillissement, tout comme le PTFE auquel il est généralement associé. Le premier bâtiment permanent utilisant une telle membrane date de 1973 et l'on n'a pas constaté à ce jour de dégradation.
Le PTFE, polytétrafluoroéthylène, est plus connu sous le nom de marque Téflon, celui-là même qui est employé dans les poêles antiadhésive, les rubans d'étanchéité pour la plomberie, ou encore comme patins glissants pour déplacer des meubles. Cette variété d'usages témoigne de ses étonnantes propriétés, entre autres: il est presque complètement inerte chimiquement c'est-à-dire qu'il ne dégaze pas et ne réagit pratiquement avec aucun produit chimique; il est antiadhésif donc autonettoyant; il est non combustible, extrêmement résistant à l'humidité et aux ultraviolets. En contrepartie il est plus cher et plus difficile à travailler. Remarquons qu'il existe une variante complètement transparente, l'éthylènetétrafluoroéthylène ou ETFE, connu sous le nom de marque Tefzel. Lui aussi a depuis quelques années un usage en architecture que l'on étudiera dans la quatrième partie.
Voici comparées les principales caractéristiques de ces deux membranes:
|
polyester-PVC |
tissu de verre-PTFE |
|
|
durée de vie |
10-15 ans |
25-30 ans |
|
coût |
bon marché |
4 à 5 fois plus cher |
|
résistance mécanique |
de 60 à 120 kg/cm pour des qualités de 800 à 1300 g/m² |
idem |
|
résistance au feu |
ne propage pas le feu et ne produit pas de gouttes incandescentes |
incombustible |
|
résistance à la salissure |
salissant voire très salissant jusqu'à prendre un aspect peu avenant |
autonettoyant |
|
résistance aux UV |
additifs protecteurs |
insensible |
|
coloration |
vaste gamme de coloris |
généralement blanc |
|
translucidité |
de 7 à 18% |
jusqu'à 25% |
|
isolation thermique |
4,5 W/m².°C pour une membrane de 1200 g/m² |
idem |
|
soudures |
légèrement moins solides que le matériau |
même résistance que la membrane |
|
pliage |
facile car souple |
difficile car reste cassant |
|
montage |
facile: l'élasticité donne une marge de manœuvre et la mise en tension se fait en une seule fois |
difficile: grande précision exigée et mise en tension progressive en plusieurs fois |
|
usage recommandé |
structures temporaires ou démontables |
bâtiments permanents |
Le matériau idéal qui allierait la facilité d'emploi et le coût avantageux du polyester-PVC avec la durée de vie et le bel aspect du tissu de verre-PTFE n'existe pas. Il existe encore moins si l'on ajoute des critères écologiques. Certes le tissu de verre n'est rien d'autre que de la silice, le matériau le plus abondant de la croûte terrestre, certes le PVC est dans une certaine mesure recyclable et le PTFE l'est complètement (tout du moins seuls, car laminés pour former des composites, c'est une autre histoire), mais dans l'ensemble l'on n'a pas affaire au summum des matériaux naturels (en précisant que le coton ne l'est pas davantage sachant qu'il est de plus en plus produit par des plants transgéniques et que cela reste le plus gros consommateur de pesticides).
Les recherches se poursuivent: fibres aramides, fibres de carbone, enduction silicone, etc. Tout ça finira bien par déboucher sur des matériaux plus satisfaisants. À moins que la surprise ne vienne d'ailleurs, de la biologie par exemple plutôt que de la chimie. J'imagine bien des colonies de bactéries synthétisant des films (et pas seulement des fils) pouvant servir directement de membranes. Des membranes respirantes, auto adaptables à des conditions de température, d'humidité et de luminosité changeantes, autoréparables même (voir http://biopro1.step.in-systeme.net/en/region/freiburg/magazin/01782/index.html?lang=en&print_style=yes). Bref une véritable peau.
À y bien regarder, un tissu n'est qu'une approximation d'une membrane puisqu'il est réalisé par tissage de fibres. On croyait l'avoir dépassé et revoilà le dilemme lignes-surfaces!
Là n'est pas le seul problème à vouloir se servir de tissu en guise de membrane. La forme architecturale à réaliser n'est jamais plate. C'est même une surface à double courbure comme on le verra plus loin. Or un tissu est toujours tissé à plat et mis en rouleaux d'une largeur donnée. La surface courbe doit donc être réalisée en assemblant des lés plats. C'est le même problème que de devoir réaliser un globe terrestre avec du papier fabriqué et imprimé à plat. En fin de compte ce n'est pas la surface idéale que l'on obtient mais une surface approchée. Plus les lés sont petits, plus l'on se rapproche de la surface, mais plus il y a de travail de découpe et de soudure. Et inversement.
Autre problème: un tissu n'est pas un matériau isotrope c'est-à-dire qu'il n'a pas exactement les mêmes propriétés dans toutes les directions. Prenez quelques échantillons de tissu, étirez-les dans différentes directions et vous constaterez que la plupart n'ont pas la même élasticité dans les deux sens. Pour comprendre il faut revenir au processus de fabrication.
Un tissu comporte des fibres orientées dans deux directions. Les fils de chaîne constituent la grande longueur d'un rouleau. Entre eux sont insérés avec la navette les fils de trame. Ils s'étirent dans la largeur du rouleau. Lors de la fabrication, le fil de trame ondule entre des fils de chaîne tendus bien droits par le métier à tisser:
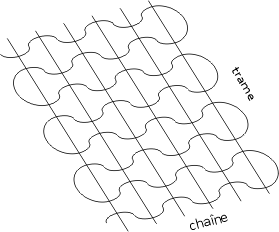
Il est évident que l'élasticité ne sera pas la même dans la longueur que dans la largeur. Dans la longueur, les fils de chaîne sont plus rectilignes, d'où une élasticité moindre; dans la largeur, les fils de trame sont plus lâches, d'où une plus grande élasticité. Conséquence: selon la manière dont un lé sera découpé dans un rouleau de tissu, il n'aura pas tout à fait les mêmes propriétés mécaniques:
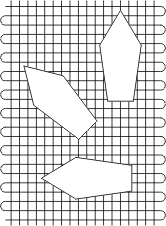
L'enduction du tissu avec un polymère quelconque ne change rien à l'affaire. En revanche on peut compliquer le tissage pour atténuer ce problème.
Vous vous souvenez de la petite expérience réalisée avec un drap dans le prologue de cette troisième partie, d'où il ressortait que plus il est tendu, mieux il résiste aux efforts. En particulier le fait de tendre la membrane lui évite de battre, phénomène très dommageable comme on le constate à l'extrémité des drapeaux qui finissent rapidement et systématiquement en lambeaux.
Autre exemple. Prenez un ballon de baudruche. Gonflez-le légèrement, juste ce qu'il faut pour lui donner forme et sentir une pression à l'intérieur. Si vous posez dessus un poids comme un dictionnaire, vous constaterez que le ballon s'écrase facilement. Il perd complètement sa forme, incapable de supporter la moindre charge.
Maintenant gonflez-le autant que vous pouvez. Vous sentez bien à l'effort que vous devez fournir la pression qui augmente à l'intérieur et la tension qui augmente concomitamment dans la membrane. Si vous reposez le livre dessus, vous constaterez cette fois que le ballon non seulement supporte facilement la charge mais qu'en plus il se déforme à peine.
Pour comprendre ce qui se passe, reprenons le schéma d'un poids suspendu à un fil étudié dans la première partie:
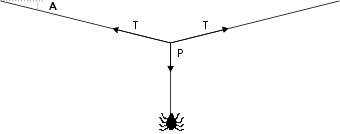
L'équilibre entre la force transversale P et la tension dans le fil T est exprimé par la formule:
![]()
Par renversement cela donne:
![]()
et s'interprète ainsi: pour une géométrie donnée (angle A donné), plus la tension T dans le câble est élevée, plus la structure est apte à supporter une charge P élevée.
Ce raisonnement appliqué à un câble se transpose facilement à une membrane. D'où il résulte que c'est la combinaison entre la géométrie (la forme de la surface) et la pré-tension de la membrane qui rend la structure capable de résister à des efforts élevés telles que surcharges de neige ou aspiration du vent. Et c'est la flexibilité de la membrane qui permet à des efforts localisés d'être dispersés dans toute la structure. Chaque fibre, lorsqu'elle subit un effort, en transfert une partie aux fibres adjacentes grâce aux variations de tension dans les fibres perpendiculaires qui les relient, et ainsi de suite jusqu'à se diffuser partout et ce faisant se diluer.
Revenons un instant à la formule ci-dessus. Pour un angle A égal à zéro, elle n'a plus de sens puisque le sinus de zéro vaut zéro. Par conséquent une telle structure ne peut en aucun cas dessiner une surface plane. Est-ce à dire que si le procédé est approprié pour couvrir l'espace il ne l'est pas pour réaliser l'équivalent d'un plancher? Non et oui. C'est sûr qu'on ne va pas pouvoir faire un étage capable de supporter des meubles traditionnels tels que lourds sommiers, commodes, penderies, etc. Mais cela n'empêche pas de réaliser une surface presque plane parfaitement utilisable, qui soit ludique (pour sauter comme sur un trampoline) autant qu'habitable (pour se reposer comme dans un grand hamac ou travailler assis en tailleur...). Remarquons que cette idée n'est pas nouvelle puisque l'espace entre les coques d'un catamaran est souvent comblé de cette manière.
On pressent que la conception de telles structures à membrane tendue n'est pas triviale du fait qu'il y a interdépendance entre la forme de la surface, la pré-tension de la membrane et ses propriétés mécaniques. Il faut particulièrement veiller à ne pas créer des zones susceptibles d'accumuler l'eau ou la neige, ni dessiner des géométries qui risquent d'engendrer des surtensions dépassant la résistance de la membrane.
Concernant ce dernier point, remarquons que l'on se donne en général une marge de sécurité de l'ordre de 6. Cela signifie que pour une membrane typique d'une résistance à la tension de 100 kg/cm (ou dix tonnes par mètre linéaire, c'est-à-dire qu'un élément de membrane d'une largeur d'un mètre peut supporter jusqu'à 10 t), la charge maximale permise est de 17 kg/cm (soit 1,7 tonnes par mètre) tandis que la charge habituelle de pré-tension est comprise entre 1,5 et 3,5 kg/cm (150 à 350 kg/m).
La conception est encore compliquée par l'anisotropie de la membrane (elle n'a pas exactement les mêmes propriétés dans toutes les directions), les discontinuités introduites par les soudures et les bords, et encore par les comportements non linéaires du matériau (les déformations ne sont pas proportionnelles à la charge).
Grâce à la modélisation informatique et à l'expérience accumulée ces dernières décennies, toutes ces difficultés sont de mieux en mieux maîtrisées. Reste que, sauf pour de très petites structures, la conception est réservée à des ingénieurs spécialisés. Preuves de leurs compétences et de la pertinence de leurs modèles, les très belles réalisations dont on a vu quelques exemples plus haut. Très belles et très résistantes, en toutes dimensions et sous tous les climats.
Une fois parvenu au bout du processus de conception, la fabrication de la membrane peut commencer. Cela se fait dans un atelier spécialisé car c'est pratiquement impossible sur le terrain. Les lès sont découpés dans des rouleaux et soudés entre eux jusqu'à former une membrane qui fait parfois plusieurs milliers de mètres carrés. Elle est pliée, expédiée sur le chantier où elle est dépliée, le tout le plus délicatement possible, particulièrement lorsque le support est en fibre de verre.
Le montage peut s'avérer lui aussi être un casse tête du fait qu'une telle structure n'est stable qu'une fois tous les éléments assemblés. C'est le même problème que rencontre un randonneur lorsqu'il se bat avec la toile et les arceaux pour monter sa tente, mais à une toute autre échelle. Et une fois le montage effectué, ce n'est pas fini car il faut encore mettre la membrane sous tension, à la valeur précise recommandée par les ingénieurs. Il faut donc aussi prévoir des vérins hydrauliques (préférentiellement sur les grandes structures) ou des tendeurs mécaniques (sur les plus petites) pour pousser les mâts vers le haut ou tirer sur les câbles.
Toutes ces complications impliquent d'intégrer dès la conception la manière dont s'effectuera le montage.
Avec les architectures à membranes modernes on s'éloigne considérablement des pratiques traditionnelles. On le pressentait mais peut-être pas à ce point. D'habitude la construction des bâtiments se fait par étapes successives simples, chacune fournissant un appui stable pour la suivante. C'est lourd évidemment mais pas compliqué. Ici c'est tout le contraire, le déploiement de la forme globale et la stabilisation de la structure se font en un seul et même mouvement. Paradoxe même, alors que le poids par mètre carré de surface couverte peut atteindre des valeurs extrêmement basses (quelques kilos seulement), on peut avoir à manipuler des éléments très lourds, quand il s'agit par exemple d'une membrane monobloc de plusieurs centaines voire plusieurs milliers de mètres carrés, sans parler des ancrages qui, comme dans un pont suspendu, assurent la jonction de la structure avec le sol. Donc tout doit être parfaitement pensé au préalable car il n'y a aucune place pour l'improvisation, une modification même minime pouvant avoir des répercussions sur le comportement de l'ensemble de la structure. C'est certes inhabituel et compliqué, mais pas impossible. La preuve, certains y arrivent. Il faut juste se donner la peine d'apprendre cette nouvelle manière de concevoir et de réaliser des bâtiments.
Il n'a été question jusqu'ici que de tension. Or l'on se doute, après toutes les considérations de la première partie, que sans quelques éléments en compression, une telle structure ne peut pas tenir. Il est facile de s'en convaincre. Revenons encore une fois au drap tendu. Disons qu'il a été attaché à des arbres. Eh bien ce sont eux qui supportent la tension de la membrane en fléchissant, conjugaison je le rappelle de tension sur le côté convexe et de compression sur le côté concave. S'ils sont suffisamment minces, cette flexion est parfaitement visible: les troncs se rapprochent en se courbant. Et si les arbres ne cassent pas ou ne tombent pas déracinés, c'est qu'ils sont solides et bien ancrés dans le sol. C'est là qu'aboutit finalement la compression. Plus exactement le sol situé entre les arbres subit un effort de compression. D'ailleurs si vous essayez de faire la même chose sur l'eau, tendre un drap entre deux voiliers par exemple, vous constaterez vite que ça n'est pas possible parce que l'eau libre ne peut pas supporter un tel effort de compression. Elle glisse, s'écarte, les deux bateaux se rapprochent, et au final le drap se pose doucement sur l'eau sans plus de tension.
Donc:
1. sans tension une membrane repose sans forme précise et se déforme à la moindre sollicitation;
2. une tension qui lui donne forme ne peut exister que si elle est contrebalancée par une compression.
Questions: quel élément prendre pour supporter cette compression et où le mettre? Si l'on pense à une tente, on voit que des mâts et des arceaux conviennent parfaitement. D'où une première possibilité pour réaliser une structure tendue, associer la membrane travaillant exclusivement en tension à des éléments rigides travaillant principalement en compression.
Est-ce tout? Il existe en fait une autre possibilité radicalement différente. Souvenez-vous du ballon de baudruche. La membrane acquiert sa tension grâce à la mise sous pression de l'air à l'intérieur. C'est donc l'air qui cette fois supporte la compression.
Question: pourquoi cet air est-il capable de supporter une compression alors que l'eau dans l'exemple du drap tendu entre deux barques en était incapable? Tout tient au fait que l'air est en surpression par rapport au milieu ambiant, grâce à la membrane qui le contient et qui par sa capacité à résister à la tension n'éclate pas sous la charge. Autrement dit les deux se tiennent mutuellement. Ce n'est pas le cas de l'air libre ni de l'eau libre. Si vous enfermiez cette dernière dans une membrane avec une légère surpression, vous auriez aussi un élément résistant en compression. Certaines piscines hors-sol par exemple sont ainsi faites: la structure est simplement un gros boudin rempli d'eau, et cela suffit à retenir l'eau du bassin et les baigneurs. Remarquons encore que la cellule, le bloc de base du monde vivant, n'est rien d'autre du point de vue structurel qu'un liquide enfermé dans une membrane sous tension.
Pour revenir à l'architecture, on va détailler maintenant les deux grandes familles de structures à membranes tendues selon la nature de l'élément qui supportent la compression: les membranes tendues sur ossature et les membranes soutenues par l'air.
Dans cette première famille de structures à membrane tendue, ce sont des éléments rigides qui supportent les efforts de compression. Elle se scinde à son tour en deux sous-familles:
1. les mâts qui sont en-dehors de la forme délimitée par la membrane,
2. les arches qui appartiennent à la surface et participent à la délimitation de la forme.
Dans un cas comme dans l'autre, une grande variété de matériaux et de procédés peuvent être utilisés, la seule chose qui compte étant que l'élément résiste à la compression. Tout ce qu'on a vu dans la première partie à propos des poutres et des arches est valable: bois brut, bois lamellé-collé, tubes métalliques, structures en treillis, arches en tensairity, en tenségrité (pas encore employé à ma connaissance mais il y a des projets), ou encore gonflables (uniquement à petite échelle, par exemple pour des tentes de secours à déploiement rapide ou pour des petits pavillons utilisés lors d'opérations promotionnelles).
La membrane d'une structure tendue sur une ossature rigide ne peut pas prendre n'importe quelle forme. Gonflez un ballon de baudruche. Il devient à peu près sphérique. Maintenant dégonflez-le et essayez d'imaginer comment reconstituer la sphère en suspendant la membrane par un nombre quelconque de points à des mâts ou des arches. Vous aurez beau tourner et retourner le problème dans tous les sens, vous n'y arriverez pas. Impossible de tendre ainsi une membrane en lui donnant une forme de sphère: ou bien elle est tendue mais elle n'est pas sphérique, ou bien elle est sphérique mais alors elle est détendue (il n'y a toujours pas de pression à l'intérieur bien sûr), ce qui se voit au fait qu'elle flotte, qu'elle ballotte.
Pour comprendre quel genre de forme donner ce genre de structure intéressons-nous à un simple câble qui pend entre deux piquets:
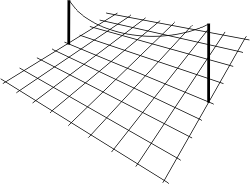
C'est comme une corde à linge trop lâche qui au moindre coup de vent s'agite dans tous les sens:
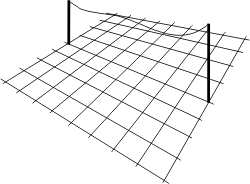
On se dit qu'il doit y avoir moyen de tenir le câble en place en fixant dessous un second câble:
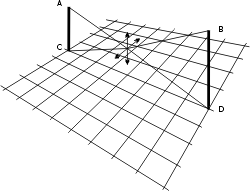
Effectivement, la structure ainsi constituée résiste parfaitement aux mouvements verticaux. En revanche elle reste très sensible à des mouvements dans un plan perpendiculaire.
Si nous orientons le câble CD dans l'autre direction, nous obtenons le résultat désiré qui est d'interdire tout mouvement:
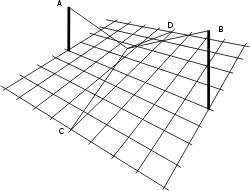
Il est intéressant de poursuivre la construction. Prenant appuis sur ces deux câbles et sur les quatre coins ABCD, il est facile d'ajouter d'autres câbles pour dessiner une surface assimilable à une membrane:
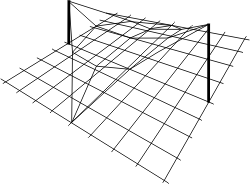 |
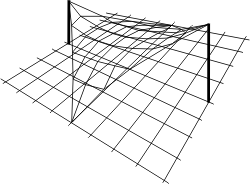 |
Voici un exemple de réalisation due à Frei Otto:
 |
Cette forme s'appelle un paraboloïde hyperbolique. Elle a des propriétés géométriques très intéressantes qui seront étudiées dans le livre suivant. En attendant retenons juste une particularité de cette surface qui saute au yeux: elle est courbée dans deux directions différentes, comme une selle de cheval. Précisément on dit qu'il s'agit d'une surface à double courbure anticlastique.
La dernière phrase du paragraphe précédent doit sûrement vous paraître incompréhensible. Je crois utile de fournir quelques explications car cela servira aussi à comprendre quelles formes peuvent prendre les structures pneumatiques. Rassurez-vous, je ne vais pas vous perdre dans des considérations mathématiques absconses. Quelques exemples simples suffiront à éclairer le sujet.
La notion de courbure d'une surface est assez facile à saisir. Il est clair par exemple qu'un plan n'a aucune courbure. Il est tout aussi clair qu'un cylindre est courbé dans une seule direction puisqu'il est droit dans l'autre. On peut d'ailleurs le réaliser en roulant une feuille de papier. Idem pour un cône. On n'a pas de mal non plus à percevoir la différence qu'il y a avec une sphère. Si l'on considère un point quelconque de sa surface, on voit qu'elle est courbée dans toutes les directions, une forme impossible à réaliser avec une feuille de papier. En mathématiques on appelle cela une surface à double courbure. Il en va de même du paraboloïde hyperbolique que l'on vient de rencontrer.
Ces deux surfaces sont à double courbure, soit, mais elles n'ont pas du tout le même air de famille. Précisément, on appelle:
- surfaces synclastiques celles où tous les rayons de courbure en un point quelconque ont leur centre d'un même côté de la surface, comme la sphère,
- surfaces anticlastiques celles où les rayons de courbure en un point sont situés de part et d'autre de la surface, comme le paraboloïde hyperbolique.
Le tore, autrement dit une surface en forme de bouée, est une figure intéressante qui va nous permettre de voir d'un peu plus près cette distinction.
Géométriquement, le tore est la surface engendrée par la rotation d'un petit cercle de centre O' et de rayon r autour du centre O à une distance R:
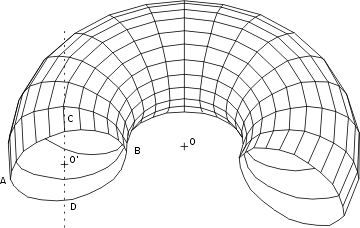
Cette surface est en tous points à double courbure. Elle présente une particularité intéressante: elle se partage en deux par un plan de coupe cylindrique vertical (représenté par la droite CD) de telle sorte qu'elle est synclastique dans toute sa partie extérieure et anticlastique dans sa partie intérieure.
Considérons par exemple le point A. La surface y est courbée un peu comme celle d'une sphère. Il est facile de voir que tous les rayons de courbure en ce point sont situés à droite de la surface. En particulier: dans le plan vertical il y a le petit cercle de centre O' et de rayon r; dans le plan horizontal le grand cercle de centre O et de rayon R+r. Tous les autres centres se promènent entre O et O'. La surface est synclastique.
Considérons maintenant le point B. La surface est courbée comme une selle de cheval. On remarque en particulier que dans le plan vertical le centre du rayon de courbure se situe comme ci-dessus en O', que dans le plan horizontal il se situe également en O, mais cette fois les deux centres se retrouvent de part et d'autre de la surface. Celle-ci est anticlastique.
Une forme convenable pour une structure tendue sur ossature rigide est nécessairement une surface à double courbure anticlastique. Elle possède une autre particularité importante qui est d'être une surface minimale. Qu'est-ce à dire?
Prenez un anneau circulaire rigide et accrochez-y un hémisphère. S'il est fait dans un matériau souple, par exemple du plastique ou du tissu, vous pouvez facilement l'enfoncer comme ceci:
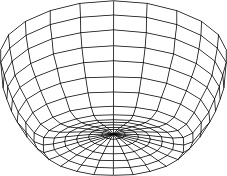
Autrement dit il se déforme sans effort et sans que sa superficie totale ne change.
Considérez maintenant le disque qui remplit la surface de l'anneau comme la membrane d'un tambour. Si vous voulez le déformer, vous devez cette fois appuyer fort, même si ce n'est du tissu. Cela est dû au fait que le disque est la surface minimale qui remplit l'anneau circulaire. Il ne peut être déformé qu'en augmentant sa superficie, ce qui est possible dans une certaine mesure en jouant avec l'élasticité du matériau. Pour mémoire la superficie du disque vaut o r² contre 2o r² pour celle de l'hémisphère.
La surface minimale est évidemment plus complexe pour des contours plus tarabiscotés qu'un cercle dans un plan mais l'idée est la même, à savoir:
- la surface minimale qui s'appuie sur ce contour ne peut se déformer qu'en augmentant sa superficie,
- une surface non minimale de ce contour peut se déformer sans modification de sa superficie.
On voit l'intérêt pour les structures tendues. Si la surface que dessine la membrane n'est pas minimale, elle va battre dans le vent et finir en lambeaux, comme tous les drapeaux. Tandis que si sa surface est minimale, elle va se déformer par élasticité du matériau, comme un ressort que l'on tend, et puis revenir à sa position initiale. La structure reprend toujours sa forme.
Cette notion de surface minimale a un autre intérêt. Nous avons vu que l'élaboration de la forme d'une structure tendue est loin d'être simple. Elle se fait de nos jours par modélisation numérique grâce aux progrès conjugués des modèles de simulation et de la puissance des ordinateurs. Mais il existe un autre moyen qui ne nécessite aucune connaissance mathématique ni aucun calcul. Il suffit d'un peu d'eau savonneuse, à condition de savoir qu'un film de savon qui se dépose sur un contour quelconque dessine automatiquement une surface minimale. C'est le procédé employé par Frei Otto pour concevoir ses structures tendues avant l'ère de la modélisation numérique. Certes l'analyse des comportements est moins poussée, mais cela permet tout de même de concevoir des structures tendues très complexes et qui tiennent. Concrètement:
1. un premier modèle est réalisé en tulle pour définir l'apparence général et préciser certains paramètres importants tels que hauteur maximale, hauteur et largeur des passages, etc.;
2. un contour en fil de fer épousant cette forme est réalisé puis plongé dans de l'eau savonneuse:
 |
3. la forme ainsi dessinée est nécessairement une surface minimale mais elle n'est peut-être pas exactement celle désirée; en jouant sur la hauteur des mâts, leur position, celle des points d'ancrage, on la déforme jusqu'à la faire correspondre au premier modèle;
4. un nouveau modèle plus précis est réalisé avec à nouveau une membrane en tulle:
 |
la membrane est fixée par des petits ressorts aux points d'ancrage qui peuvent être légèrement déplacés; on procède à de petits ajustements pour assurer une distribution uniforme des tensions et la régularité de la surface;
5. la forme étant précisément définie, les lés qui serviront à réaliser la membrane sont délimités.
Il y a évidemment un nombre infini de formes qui ont la propriété d'être des surfaces à double courbure anticlastiques. En pratique, les architectes se contentent souvent des mêmes formes plaisantes et éprouvées que l'on sait maintenant parfaitement calculer. En les déformant, les tronquant, les orientant de diverses manières, les assemblant entre elles, cela offre déjà beaucoup de possibilités. Citons notamment:
Le paraboloïde hyperbolique que l'on a déjà rencontré.
Le cône, pas le cône classique à côté droit bien sûr mais à côté arrondi pour dessiner une surface à double courbure anticlastique. C'est sans doute la forme la plus simple avec sa symétrie circulaire et son unique mât central. En voici une variante sur une base hexagonale:
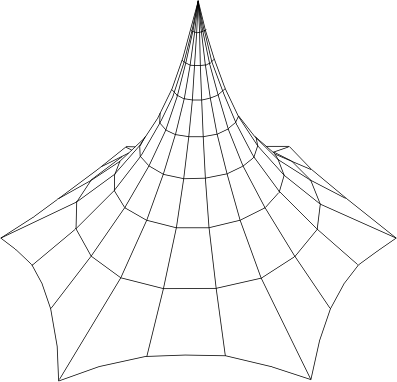
On remarque les bords courbes parce qu'ils sont supposés maintenus par un câble (le rebord de la membrane est replié pour former une gaine dans laquelle est inséré un câble qui est ensuite fixé par ses deux extrémités et tendu).
Voici également le patron de cette forme, plus précisément des trois lés qui constituent chacun des six panneaux identiques de ce cône hexagonal:
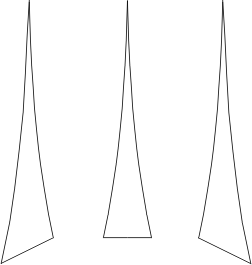
L'arche:
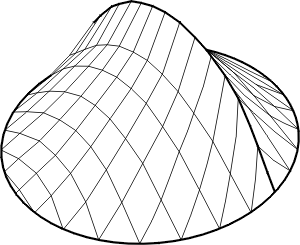
Sont mis en évidence sur ce schéma l'arche unique en arc de cercle et l'anneau de compression qui constitue la base circulaire. On voit bien comme ces deux éléments de l'ossature sont partie intégrante de la surface, contrairement aux mâts des formes précédentes. Ceci est l'exemple le plus simple d'arche mais on peut lui donner d'autres formes (elliptique, parabolique, funiculaire, etc.) et en mettre autant qu'on veut en les orientant dans diverses directions:
- les disposer verticalement et parallèlement de manière longitudinale comme dans les longues serres,
- les disposer verticalement de manière radiale comme les baleines d'un parapluie (même si dans cette configuration ça ressemble davantage à une sphère, la surface reste en tous points anticlastique, il suffit d'observer la courbure que prend la membrane d'un parapluie ouvert pour s'en rendre compte),
- les incliner comme sur une capote de landau.
À superficie égale les formes anticlastiques sont moins habitables que les formes synclastiques. Il suffit de comparer la figure précédente avec un hémisphère qui s'appuierait sur le même anneau. De l'intérieur de l'hémisphère on a l'impression d'un volume ouvert, tandis qu'il se referme dans l'autre cas.
Plus subtilement, de telles structures tendues procurent des sensations qui ne sont pas familières. Je parle de structures relativement importantes dans lesquelles la traction sur les ancrages se mesure en tonnes et non pas en kilos. D'une part il y a justement la présence de ces ancrages, souvent très imposants, qui viennent contredire la sensation de légèreté. D'autre part la tension qui habite la membrane et les câbles est parfaitement perceptible, s'ils ne sont pas dissimulés par des faux plafonds et autres cloisons. On sent une énergie contenue qui n'est pas celle de l'arc bandé prêt à lancer sa flèche, ni celle de la voile gonflée qui propulse un navire. Nous n'avons pas encore les repères pour sentir que cette énergie ne sert à rien d'autre qu'à conférer sa résistance à la structure. Je n'ai pas connaissance de personnes ayant choisi d'habiter en permanence dans de tels bâtiments. Je ne sais donc pas si avec l'habitude la perception se modifie au point que cette tension n'est plus ressentie comme étrange mais plutôt comme utile voire agréable, à l'instar d'une voile. À suivre donc...
De l'air sous pression retenu dans une enveloppe en tension, voilà qui suffit pour avoir un élément de structure résistant à la compression. Cette famille de structures se scinde en trois sous-familles:
1. les structures gonflables (air inflated structures en anglais)
Ce sont de véritables poutres ou arches qui tiennent grâce à une pression de plusieurs centaines de grammes par centimètre carré. S'y rattachent aussi les systèmes hybrides en tensairity. Tout ceci a été vu dans la première partie. Comme n'importe quel type de poutre ou d'arche, ces éléments peuvent être associés à des membranes pour réaliser des structures tendues dont ils constituent l'ossature.

2. les membranes soutenues par l'air (air supported structures en anglais)
Cette fois, c'est la totalité de la membrane constituant la couverture du bâtiment (voire le bâtiment en entier lorsque murs et toit se confondent) qui est mise sous pression. Quelques grammes par centimètre carré suffisent pour assurer la tenue d'une structure de plusieurs centaines, plusieurs milliers voire dizaines de milliers de mètres carrés. C'est le sujet de ce chapitre.
3. les coussins gonflables (air pillows ou pneumatic cushions en anglais)
Ce ne sont pas des éléments structuraux mais des éléments de couverture qui fonctionnent eux aussi à basse pression, quelques grammes. Ils seront étudiés dans la quatrième partie.
Ballons et dirigeables peuvent être considérés comme les précurseurs des structures à membrane soutenue par l'air. L'idée de transposer ces procédés à l'architecture semble avoir germé en premier dans la tête d'un ingénieur britannique du nom de Lanchester. En 1917 il dépose un brevet pour un hôpital de campagne constitué d'une membrane soutenue par l'air. Problème de matériaux ou problème de demande? toujours est-il qu'il n'a pu réaliser son rêve.
Il a fallu attendre la fin de la deuxième guerre mondiale pour voir la réalisation effective de structures architecturales à membranes soutenues par l'air. Le maître d'ouvrage en était l'armée américaine qui commençait à installer d'énormes radars pour surveiller sa frontière nord, très proche de l'URSS vue depuis l'arctique. Les conditions climatiques difficiles, la fragilité des antennes, et la nécessité d'une structure et d'une couverture non métalliques pour rester transparentes aux ondes électromagnétiques ont conduit à choisir la solution proposée par Walter Bird: un dôme gonflable. Première réalisation en 1948: un dôme de 15 mètres de diamètre fait d'une membrane de tissu de nylon enduit de vinyle qui passe avec succès les tests. En quelques années des centaines de radômes, ainsi qu'on les appelle, sont érigés en Alaska et au Canada. Du coup Bird fonde sa propre compagnie, Birdair, en 1956.
Ces radômes par leur forme ne sont pas très éloignés de leurs ancêtres les ballons. Une différence importante toutefois concernant le principe de fonctionnement:
- dans un ballon on n'introduit pas de surpression à l'intérieur par rapport à l'extérieur, c'est une différence de densité qui assure la portance (dans un ballon à air chaud elle est créée par une différence de température);
- dans une structure pneumatique il y a surpression de l'air intérieur par rapport à l'extérieur pour donner simultanément forme et tenue.
Contrairement à ce qu'on pourrait croire cette surpression n'est pas du tout gênante pour les occupants. En fait elle est si minime qu'on ne sent rien en passant du dehors au dedans et inversement (en général à travers un sas constitué de portes tournantes). À peine 2 pour mille de surpression suffisent pour tenir la structure, soit 2 ou parfois 2,5 g/cm². C'est de beaucoup inférieur aux fluctuations de la pression atmosphérique dont l'amplitude dépasse 40 g/cm² entre anticyclones et dépressions. Deux grammes par centimètre carré, c'est la différence de pression existant entre le rez-de-chaussée d'un immeuble et le quatrième ou le cinquième étage. C'est encore la surpression qui règne à 2 cm sous l'eau. Rien de notable donc.
Remarquons que si une pression de 2 g/cm² soutient un toit de 20 tonnes, il n'y a pas à fournir un effort aussi colossal pour que ça tienne. Concrètement, supposons qu'un ventilateur de 1,14 mètre de diamètre serve à maintenir la pression. La force contre laquelle il a à lutter pour forcer l'air à l'intérieur est seulement de 20 kg (la pression multipliée par la surface qui est ici de 1 m²). Donc pas besoin d'un turboréacteur pour insuffler l'air qui tient la membrane. Le seul problème est de bien dimensionner l'installation de soufflage pour compenser les pertes naturelles (porosité de la membranes, ventilation, entrées et sorties des personnes par les sas) plus d'éventuels aléas (comme des petites déchirures ou des décrochages localisés de la membrane).
Comme dans un ballon de baudruche, la membrane est mise en tension par la pression de l'air, et cette mise en tension lui confère aussi sa forme. Tous ces paramètres se combinent de sorte que, en gros, la tension est proportionnelle à la pression et au rayon de courbure. Précisément dans le cas simple d'une sphère (simple parce que tous les rayons de courbure en un point sont identiques et égaux au rayon de la sphère), on a:
![]()
Pour fixer les idées, la tension s'exerçant sur la membrane d'un dôme hémisphérique de 10 m de rayon sous une pression de 2 g/cm² est de 1 kg/cm. Autrement dit une force de traction de 1 kg seulement s'exerce sur un bout de membrane de 1 cm de largeur. Pour un hémisphère de 100 m de rayon, la tension augmente pour atteindre 10 kg/cm. Cela reste raisonnable, sauf que sur des très grandes structures toutes ces tension élémentaires s'additionnent pour atteindre au bout du compte des valeurs considérables, plusieurs centaines de tonnes. D'où la présence fréquente de câbles d'acier passant par-dessus la membrane. Ils ne sont pas là pour participer à son soutien, puisqu'ils n'ont pas plus de résistance qu'elle à la compression, mais à la soulager d'une partie de cette tension.
Le problème d'une telle structure n'est pas qu'elle pèse sur le sol mais qu'elle a tendance à s'envoler. Pour reprendre les exemples ci-dessus, la force totale qui s'exerce du bas vers le haut est de 6280 kg pour le dôme de 10 m de rayon et de 628 t pour celle de 100 m. Ramenée au mètre linéaire de la base circulaire, cela fait une force de soulèvement de 100 kg/m dans le premier cas et de 1000 kg/m dans le second. Si l'on tient compte aussi des forces d'aspiration du vent, il faut multiplier ces chiffres au moins par trois pour assurer un ancrage au sol satisfaisant.
Du coup la légèreté en prend un sérieux coup. Certes la membrane est légère (autour de 1 kg/m² sans compter les câbles éventuels), certes l'air qui tient toute la structure en étant à peine comprimé est léger (environ 1,3 g/l) mais l'ancrage lui est forcément lourd et il est partie intégrante de la structure, troisième élément aussi indispensable que les deux autres. Renversement complet de logique par rapport aux empilages: ce qui délimite la surface est très léger, tellement qu'un énorme poids au sol est nécessaire pour l'empêcher de s'envoler!
Pour fixer les idées considérons encore une fois un dôme hémisphérique de 10 m de rayon. La membrane pèse environ 628 kg (en prenant pour base 1000 g/m²) soit beaucoup moins que le poids du volume d'air qu'elle renferme, un peu plus de 2000 mètres cubes pesant près de 2700 kilos. Quelle maison de plus de 300 m² peut se targuer de peser moins d'une tonne, moins que le poids de l'air qu'elle contient? Sauf qu'il faut ajouter près de 20 tonnes pour l'ancrer au sol. Pas très léger finalement!
Considérons ces deux exemples d'un hémisphère au sommet enfoncé et d'un cube (images de gauche):
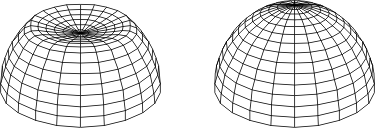
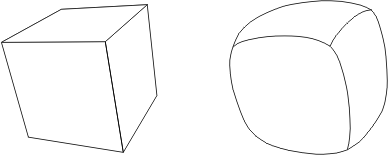
Si nous mettons la pression, ils se déforment comme on le voit à droite. Conclusions:
- certaines formes anticlastiques (une partie de la sphère enfoncée est anticlastique) ne tiennent pas sous la pression,
- les forment planes (comme les faces du cube) ne tiennent pas sous la pression,
- la mise sous pression déforme une surface et tend à la rapprocher d'une sphère,
- des plis peuvent apparaître lors de cette déformation parce que la forme de la surface et celle de son contour ne correspondent plus.
La forme d'une structure pneumatique doit être au moins en partie synclastique. Les surfaces purement anticlastiques comme le paraboloïde hyperbolique sont impossibles à réaliser. Il n'est toutefois pas interdit que certaines parties soient anticlastiques. Preuve en est le tore: entier il forme une bouée; placé horizontalement et coupé horizontalement par le milieu cela fait une sorte de tunnel circulaire; placé verticalement et coupé en deux horizontalement cela fait une arche.
Retenons surtout que toutes les formes ne sont pas possibles pour des structures pneumatiques et qu'elles sont à prédominance synclastique.
Voici un petit test simple pour savoir si une forme peut être réalisée pneumatiquement: si l'on prend une sphère dont le diamètre varie en continue le long d'un trajet quelconque, la surface enveloppe ainsi engendrée peut être formée pneumatiquement. Deux exemples, le premier montrant une vue en coupe latérale d'une structure verticale à symétrie circulaire, et le second une vue de dessus d'une sorte de tunnel serpentin à section semi circulaire:
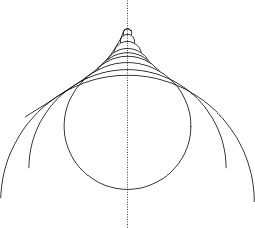
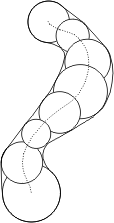
La conception est compliquée par le fait que la membrane réelle n'est qu'une approximation de la forme idéale puisqu'elle est réalisée à partir de lés plats. Et pour compliquer encore davantage les choses, il faut noter que la forme dépend de la charge, laquelle se décompose en charge permanente due à la surpression (comme un ballon de baudruche change de forme en augmentant ou diminuant la pression, quoique ici la membrane ayant une élasticité moindre subit des déformations comparativement plus faibles mais difficiles à prendre en compte du fait qu'elle a un comportement non linéaire) et surcharges temporaires provoquées par le vent ou des accumulations de neige (voir plus haut l'expérience du livre posée sur un ballon de baudruche). Suite à ces changements de forme des plis peuvent apparaître. On observe bien la formation de tels plis lorsqu'on gonfle plus ou moins une bouée. En ces points la tension augmente ou diminue, ce qui dans tous les cas se traduit par une fragilisation de la membrane. Toutes ces difficultés expliquent que l'on s'en tient en général à des formes banales dérivées plus ou moins du cercle.
Les réalisations se regroupent en deux familles: les bâtiments à profil haut et les toits à profil bas.
Les premiers correspondent à un rapport hauteur/largeur assez élevé, de l'ordre de 1 ou 1/2. La membrane tient lieu à la fois de toit et de mur. La portée est limitée à quelques dizaines de mètres et le rayon de courbure est assez court, d'où des tensions qui restent faciles à maîtriser (je rappelle que la tension est proportionnelle au rayon de courbure). Surtout si l'on ajoute la simplicité des formes, globalement arrondies sur une base circulaire (radômes), elliptique ou rectangulaire (servant généralement d'entrepôts ou de couverture pour des courts de tennis).

Les structures à profil bas ont quant à elle un grand rayon de courbure au point qu'elles apparaissent relativement peu bombées. Elles servent surtout de toits qui viennent couvrir des grands édifices existants tels que des stades. Les portées permises par cette technologie sont énormes. Le Pontiac Silverdome Stadium de Détroit est muni d'un tel toit fait d'une membrane de tissu de verre enduit de téflon de 229 mètres sur 168, soit près de quatre hectares. C'est l'un des plus anciens du genre (1975) mais pas le plus grand. Il faut ajouter 18 gros câbles d'acier qui reprennent la tension et 29 ventilateurs géants dont trois seulement servent en temps normal à maintenir la légère surpression de quelques grammes par centimètre carré.
 |
Même si le concept de membranes soutenues par l'air est séduisant et que de nombreuses réalisations ont fait leurs preuves, le bilan déçoit quelque peu:
- le bénéfice de la légèreté est annihilé par l'indispensable présence de pesants ancrages pour retenir la membrane de s'envoler;
- il faut obligatoirement un système actif (capteurs de pression et ventilateurs) pour maintenir la surpression à l'intérieur; en cas de panne la structure s'effondre en quelques minutes (même si c'est généralement sans danger étant donné le faible poids de la membrane, sauf s'il y a des tonnes de neige accumulées dessus);
- une construction très soignée est exigée pour réaliser une bonne étanchéité sur tout le pourtour de fixation de la membrane;
- les formes sont limitées et beaucoup moins séduisantes que celles permise par la présence d'une ossature.
Tout ceci explique probablement que ces structures restent cantonnées à quelques domaines très particuliers pour lesquels il n'y a guère d'autres solutions. Par exemple couvrir plusieurs hectares d'un seul tenant, sans appui intermédiaire et à un coût attractif.
Les structures à membranes tendues, qu'elles prennent appui sur des éléments rigides ou sur de l'air comprimé, se heurtent on l'a vu à un paradoxe: elles sont ce qui se fait plus léger pour couvrir l'espace (de l'ordre du kilogramme par mètre carré pour la membrane seule) mais nécessitent en même temps de lourds ancrages au sol. D'où l'envie de se débarrasser de ces ancrages pour parvenir enfin à une vraie légèreté. L'exemple suivant emprunté au domaine connexe des ouvrages d'art suggère que ce devrait être possible.
Voici le schéma d'un pont suspendu:
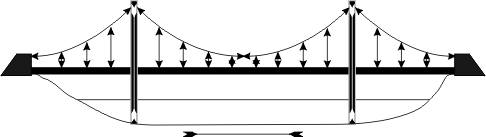
Le poids du tablier est pris par les câbles verticaux puis repris par les grands câbles en parabole. La tension dans ces câbles est transformée: d'une part en forces verticales de compression sur les piles, et d'autre part en forces de traction au niveau des extrémités. Selon l'angle avec lequel les câbles sont fixés aux culées, ces dernières peuvent comporter une petite composante verticale de soulèvement, et surtout, dans tous les cas, une importante composante de traction horizontale. La première est compensée par le poids même de la culée. Mais quid de la composante horizontale? En fait c'est la Terre elle-même qui intervient, comme une gigantesque poutre en compression placée sous le pont. Les culée, par leur poids, servent à relier les câbles à la Terre. Celle-ci ne se contente pas de porter le poids du pont, elle fait elle-même partie de la structure. Sans sa participation à l'absorption des forces de traction horizontales, le pont ne tiendrait pas.
Voici maintenant un pont à haubans:
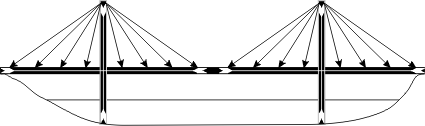
Au premier coup d'œil la différence ne semble pas bien grande: on retrouve des piliers, un tablier, et des câbles pour le supporter. En fait les deux sont très différents du point de vue structurel. De part et d'autre de chaque pilier le tablier est maintenu en équilibre comme les plateaux d'une balance par des câbles qui rayonnent symétriquement. La Terre n'est plus là que pour porter le poids et ne participe d'aucune autre manière à la structure. Plus besoin de culées.
Insistons sur le fait que cet important changement de comportement structural a été obtenu très simplement en modifiant seulement la manière dont les câbles sont accrochés.
Y aurait-il de même quelques moyens simples de rendre les structures tendues plus autonomes vis-à-vis de la Terre, conduisant ainsi à faire l'économie des lourds ancrages? La transposition de l'exemple ci-dessus sera plus facile à comprendre si l'on passe par une étape intermédiaire, la roue de bicyclette, ou pour être plus précis la roue à rayons.
On a tous en tête le schéma d'une bicyclette et on visualise sans peine le poids du cadre et du conducteur pesant sur les roues au niveau de leur moyeu. Question: comment ce poids est-il à son tour transmis au sol? Plus précisément: passe-t-il par les rayons situés dessous, qui sont donc mis en compression (figure de gauche), ou par les rayons situés dessus, qui agissent comme des câbles en tension (figure de droite)?

En fait la figure de gauche montre le comportement d'une roue de charrette et pas celui d'une roue de bicyclette. La figure de droite montre ce qui se passe réellement dans une roue à rayons:
1. le moyeu est suspendu à la jante par le rayon du dessus,
2. du coup la jante tend à s'écraser, à s'ovaliser,
3. mais les rayons horizontaux se mettent à leur tour en tension et limitent sa déformation.
Bref, les rayons pourraient être remplacés par des câbles, la roue fonctionnerait tout aussi bien. Sauf qu'elle serait plus difficile à monter et à régler, c'est pourquoi l'on préfère finalement employer des petites tiges métalliques. Mais l'important demeure, à savoir que dans une telle roue seule la jante travaille en compression tandis que les rayons travaillent en tension. En outre elle est autonome du point de vue structurel, sinon la bicyclette ne roulerait pas.
Des ingénieurs ingénieux (tous ne le sont pas) ont trouvé plusieurs façons de transposer cette idée aux structures tendues. En voici deux.
Ce mot signifie ˝nuage flottant˝ en japonais. Une image évocatrice de l'impression qu'offre au visiteur cet énorme toit conçu par Daiichi-Kobo en 1997 pour couvrir sur plus de deux hectares le stade de Kumamoto au Japon.

Les schémas suivants en décrivent le principe:
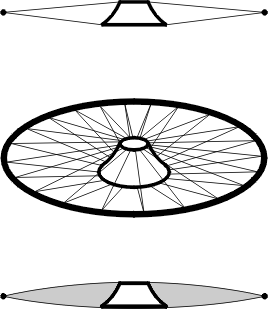
La structure se présente comme une énorme roue à rayons placée horizontalement: un anneau de compression extérieur tenant lieu de jante, un moyeu de forme particulière, et 52 câbles qui les relient par le haut et par le bas (tous ne sont pas représentés pour des raisons de lisibilité). Entre les deux rangées de câbles prend place une sorte d'énorme bouée gonflable en tissu de verre enduit de téflon. Une pression de 3 g/cm² suffit pour lui faire prendre sa place entre les câbles et lui faire épouser le moyeu. L'air insufflé met la membrane en tension qui met à son tour les câbles en tension et c'est ce qui donne à la fois forme et tenue au ˝nuage flottant˝.
Quelques autres caractéristiques intéressantes:
- le bâtiment fait plus de 26 000 m² et la surface couverte par la membrane en représente plus de 23 000, soit près de 170 m de diamètre à une hauteur de 48 m;
- le toit pèse près de 1000 tonnes, ce qui paraît beaucoup mais représente seulement 45 kg/m², tout compris c'est-à-dire la membrane plus les câbles plus le moyeu plus la jante; c'est plus lourd évidemment qu'une membrane seule mais le système est complètement autonome et ne nécessite aucun ancrage, seulement des supports;
- la membrane n'étant pas soutenue par l'air mais gonflée comme une bouée, il n'y a pas de risque d'effondrement en cas de grosse déchirure ou de panne d'électricité; comparativement à une simple membrane supportée par l'air, un débit d'air 40 fois moindre suffit pour compenser les fuites et maintenir la pression dans cette double enveloppe de plusieurs dizaines de milliers de mètres cubes (un peu plus de 4000 mètres cubes par heure).
Quoique s'inspirant lui aussi de la roue à rayons, David Geiger propose une solution très différente:
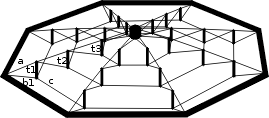
On retrouve un anneau de compression, un moyeu et des câbles, mais disposés différemment et avec en plus quelques tiges rigides en position verticale. Voici comment cela marche:
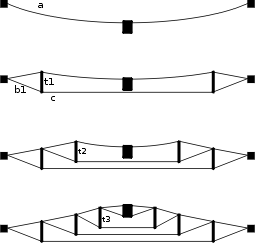
1. l'anneau de compression et le moyeu sont positionnés, les câbles radiaux suspendus;
2. les tiges de la première série (t1) sont accrochées aux câbles par le haut; elles sont en outre reliées par leur extrémité inférieure à l'anneau de compression par des petits câbles (b1); ensuite est fixé le câble périphérique (c); mis en tension, il stabilise le premier anneau de la structure;
3. l'opération est répétée avec la deuxième puis la troisième série de tiges;
4. la structure achevée, la membrane vient la recouvrir.
La première construction de ce genre a été réalisée pour couvrir la salle de gymnastique des jeux olympiques de Séoul en Corée. D'autres ont suivi. Particulièrement remarquable, le toit du Tropicana Field de St Petersburg en Floride d'une portée de plus de 200 m pour un poids de moins de 25 kg/m².
Notons qu'il ne s'agit pas d'une structure à membrane tendue à proprement parler mais plutôt d'une structure à câbles tendus. C'est seulement une remarque en passant, pas une critique, car il ne s'agit pas d'être dogmatique mais pratique. Et de ce point de vue, nul doute que c'est une réussite.
L'imagination des ingénieurs ingénieux n'étant jamais en panne, voici une autre proposition radicalement différente pour rendre des structures à membrane tendue autonomes vis-à-vis de la Terre. Elle est l'œuvre de Bob Gillis, fondateur de Shelter Systems (http://www.shelter-systems.com d'où sont tirées toutes les informations de ce paragraphe ainsi que la photo). Sa solution s'inspire à la fois du dôme géodésique et de la tenségrité pour arriver à un dôme hémisphérique où une membrane donne forme à des arches flexibles tout en étant soutenue par elles. Les dimensions sont modestes comparées aux grandes réalisations précédentes mais néanmoins supérieures aux ordinaires tentes de camping. La plus grande fait 10 m de diamètre (30 pieds), soit une surface couverte d'environ 75 m², tout en étant très légère à tous les sens du terme: moins de 100 kg pour l'ensemble arches et membrane, et un prix de vente de moins de 2000$.
Bob Gillis n'est pas un novice en matière de conception de tentes. On lui doit en 1976 la première tente de randonnée fondée sur les géodésiques et la tenségrité. De nombreux modèles commerciaux de tentes de randonnée à arceaux flexibles exploitent l'un ou l'autre de ses brevets. Mais cette fois il s'agit d'autre chose, proposer au grand public des structures plus grandes et pour des usages variés: de l'habitation permanente à l'abri d'urgence, de la salle de jeux à l'abri piscine, de la serre au solarium en passant par l'observatoire astronomique et quantités d'autres usages.

Ses dômes comportent de nombreuses innovations simples mais intéressantes:
forme
Voici le patron permettant de définir la surface de la membrane (pour les dômes les plus courants de 14, 18 et 20 pieds de diamètre, les modèles plus grands et plus petits étant basés sur d'autres configurations):
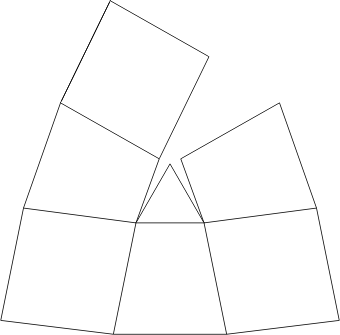
Quatre panneaux de ce genre pliés et assemblés permettent de réaliser un dôme inscrit dans un hémisphère:
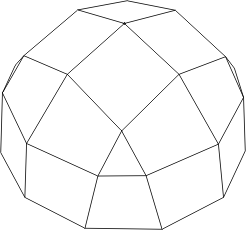
D'accord ce n'est pas une forme très originale même si cela se démarque du classique dôme géodésique. La conception de la structure l'est davantage.
arches
La principale innovation concerne les arches. L'idée consiste à employer un matériau flexible pour réaliser véritablement des arcs, courbés comme les armes du même nom par un élément en tension, ici une membrane au lieu d'une corde:
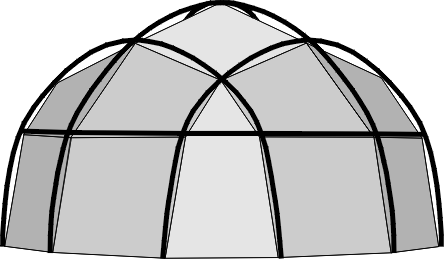
On remarque que la membrane est située sous l'ossature. L'ensemble constitué par la membrane et les arches est à sa manière un système en tenségrité. En particulier il est totalement autoportant. Le dôme peut être soulevé, déplacé, retourné même, sans rien perdre de sa forme.
Pour des raisons de coût, de facilité de transport et de montage, les arches ne sont pas d'un seul tenant (ce serait possible en utilisant par exemple la fibre de verre, comme les perches des sauteurs) mais constituées d'éléments courts (autour d'un mètre cinquante) ajustés en longueur au patron de la forme et assemblés grâce à des connecteurs spéciaux.
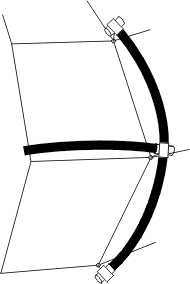
Il est intéressant de remarquer que, contrairement à un dôme géodésique classique formé de triangles, la plupart des tiges ont ici la même longueur.
matériaux
Le choix de matériaux courants rend ces constructions extrêmement faciles à réaliser, à réparer, à monter et à démonter (1/2 heure sans outils), et finalement très peu onéreuses (quelques centaines de dollars).
Pour les arches, des tubes de plomberie en PVC de 1" class 200 ou class 125 (il s'agit de normes américaines qui correspondent à ceci: diamètre extérieur 3,34 cm, diamètre intérieur 2,97 cm, résistance à la pression 14,4 et 9 kg/cm² respectivement).
Pour les connecteurs, des tubes PVC de même catégorie mais de diamètre immédiatement supérieur (1"1/4) dans lesquels viennent s'emboîter les précédents. Ils consistent simplement en deux bouts de tuyau coupés à la longueur de 12,5 cm et fixés en croix.
L'accrochage de la membrane aux tubes se fait grâce à des petits dispositifs en plastique appelés Grip-Clip et développés tout spécialement. Ils évitent de percer la membrane (inconvénient des œillets).
La membrane est faite d'une matière plastique travaillée selon un procédé appelé ripstop qui la rend très résistante à la tension et quasi indéchirable. On commence par fabriquer un film plastique que l'on étire jusqu'à ce qu'il perde une grande partie de son élasticité sans amoindrir sa résistance. Le film est alors coupé en fines lanières qui sont tissées. Le tissu ainsi obtenu est laminé sur ses deux faces avec des films étirés comme précédemment et incorporant des protecteurs UV. On obtient de la sorte une membrane résistant bien à la tension, indéchirable (on peut la percer bien sûr mais la déchirure ne se propage pas, même sous tension), relativement durable, disponible en plusieurs coloris (translucide, blanc, noir, argent), et très bon marché (moins de 10$ le mètre en 1,5 m de large).
Si j'insiste particulièrement sur cet exemple c'est que, contrairement à ce qu'on aurait pu craindre à la lecture de tout ce qui précède, il prouve que les architectures à membrane tendue ne sont pas réservées à des édifices monumentaux d'une complexité et d'un coût exorbitants, ni à de minuscules tentes de randonnée inutilisables en-dehors de l'usage pour lequel elles sont prévues. Bob Gillis s'est donné la peine de pénétrer les principes qui régissent les structures légères et il est parvenu à une solution très simple et très efficace (avec tout de même quelques limitations dans des conditions climatiques extrêmes). Ce faisant il ouvre une voie à d'autres chercheurs qui voudront bien à leur tour se creuser la tête pour nous proposer d'autres solutions tout aussi simples, encore plus efficaces et si possible plus élégantes. Il ouvre aussi la voie à une véritable démocratisation des structures à membrane tendue.
Les structures à membrane tendue deviennent de plus en plus courantes dans le paysage architectural:
- grandes structures tendues sur ossature: gares, aéroports, salles de sports, etc.
- petites structures supportées par l'air: abris de tennis ou de piscines
 |
- petites structures tendues sur ossature: tentes de randonnée et de camping, pavillons d'expositions ou de loisirs
 |
|
De là à accepter ces structures en guise d'habitations, le pas est encore grand. Je n'ai connaissance que d'une personne en France qui habite de manière permanente dans un dôme gonflable et aucune dans une structure tendue sur ossature (une grande s'entend, pas juste une toile posée sur des cordes ni une tente de camping à arceaux). Pourtant le catalogue des formes est vaste et attrayant, et les difficultés techniques ne semblent guère plus élevées que pour les dômes géodésiques. Quantité de tels dômes ont été érigés par des autoconstructeurs, alors pourquoi tant de freins vis-à-vis des architectures à membrane? J'en vois deux, le premier psychologique, l'autre technique.
Nous sommes partis de la tente noire des nomades du désert, de conception simple, relativement facile à fabriquer (pour qui sait tondre les chèvres et les moutons, filer la laine et la tisser), mais pas très grande (on n'y tient debout qu'en son centre) ni très confortable hors de son contexte géographique, climatique et d'un mode de vie d'éleveur nomade. Nous avons fini sur une tente d'un autre genre, le dôme à membrane en tenségrité développé par Shelter Systems, encore plus facile à construire (pour qui a un magasin de bricolage à côté de chez lui), sans doute plus confortable dans d'autres contextes que le désert aride, mais pas très originale du point de vue morphologique, pas très avenante avec sa simple peau de plastique, ni résistante à des conditions extrêmes. Bref, l'œil du novice ignorant tout de la tenségrité et autre subtilités structurales n'y verra guère plus qu'une tente de camping améliorée. Voilà justement ce qui me semble être le premier frein à la démocratisation des architectures à membrane, leur assimilation à la tente, avec tout ce que cela sous-entend en termes de petitesse, d'inconfort et de fragilité. Pour quelques nuits, pourquoi pas, mais en guise d'habitation permanente, pas question!
Pourtant nous savons maintenant que les architectures à membrane ne sont pas toujours synonymes de tentes. Nous avons rencontré des édifices qui par leurs dimensions impressionnantes, jusqu'à plusieurs hectares, leurs formes originales souvent très élégantes et leur durabilité n'ont plus grand chose à voir avec les tentes, qu'elles soient anciennes ou modernes. Le hic est qu'elles semblent inaccessibles à l'architecte moyen et plus encore à l'autoconstructeur: difficultés de conceptions sans moyens informatiques puissants, difficultés de construction sans équipes rodées, sans parler des matériaux qui ne sont pas disponibles dans le premier magasin de bricolage venu et ne se travaillent pas dans un garage avec les habituels outils du bricoleur, perceuses, visseuse et autres scies sauteuses. Tel est me semble-t-il l'autre frein à la démocratisation des architectures à membrane, leur côté par trop high-tech.
Pourtant ces architectures à membrane ouvrent de belles perspective, notamment les structures tendues sur ossature rigide, souvent plus élégantes et moins problématiques que celles soutenues par l'air. La solution proposée par Shelter Systems montre que, malgré ses insuffisances, ces structures peuvent être simples et accessibles. Que proposer d'autre qui soit aussi accessible?
Souvenons-nous:
1. les premières réalisations de Frei Otto (y compris le monumental pavillon allemand de l'exposition universel de Montréal et la plus monumentale encore couverture du complexe olympique de Munich) emploient des câbles et des filets métalliques en guise de substituts à des membranes,
2. des réalisations plus récentes tout aussi spectaculaires comme le câble-dôme et le ˝nuage flottant˝ emploient aussi des câbles qui participent ŕ la forme et à la structure,
3. une modélisation est possible qui ne nécessite ni connaissances physiques ni recours à l'informatique, seulement un peu d'eau savonneuse déposée sur un contour métallique.
De là l'idée de revenir à des structures de câbles tendus, la membrane n'étant plus qu'une couverture qui ne joue pas de rôle structural. Ce qu'on perd d'un côté en rajoutant une couche, on le gagne de l'autre en simplifiant à la fois la conception, la réalisation, l'approvisionnement et le travail des matériaux, et finalement la maintenance. On en arrive ainsi à une structure en trois couches:
1. un réseau de câbles principaux qui supportent l'essentiel des tensions en s'appuyant sur des mâts et des ancrages;
2. un réseau de câbles secondaires formant un filet à mailles plus fines qui délimite plus précisément la forme et soulage la membrane;
 |
Frei
Otto, volière de Munich |
3. la membrane elle-même qui n'a plus qu'un rôle de protection, principalement au Soleil, à l'eau et à l'air.
On en revient en quelque sorte à une organisation hiérarchisée, mais c'est le prix à payer tant qu'on ne dispose pas d'une membrane satisfaisante apte à remplir à elle seule toutes les fonctions, y compris structurale, tout en étant bon marché, facile à travailler et si possible aussi écologique et saine. Dans ce contexte les structures à membranes fixées sur ou sous des câbles constituent un bon compromis.
montage
Le fait de réintroduire une certaine dose de hiérarchie simplifie grandement le montage qui, on l'a vu, est souvent problématique dans les structures tendues du fait de l'interdépendance entre la forme et la tension. Pour autant on ne s'éloigne pas trop de l'esprit de l'architecture à membrane dans la mesure où le réseau de câble se comporte quasiment comme une membrane. On peut le voir comme un tissu à tissage très très lâche.
forme
Une grande variété de formes est possible, aussi séduisantes les unes que les autres, qu'elles soient régulières (comme les cônes, les arches, les paraboloïdes hyperboliques) ou complètement libres (à l'exemple des réalisations de Frei Otto). On peut imiter des formes existantes en les réduisant d'échelle, ou inventer ses propres formes en les modélisant suivant la méthode décrite plus haut.
 |
Frei
Otto, volière de Munich
http://www.freiotto.com |
matériaux
Comme il s'agit de couvrir des surfaces de quelques centaines de mètres carrés tout au plus et pas des milliers, les problèmes de résistance des matériaux restent maîtrisables sans avoir recours à des produits high-tech ni des calculs poussés. Du coup ils sont relativement faciles à se procurer à un coût raisonnable.
Des poteaux électriques ou téléphoniques conviennent en guise de mâts.
Les câbles ainsi que tous les accessoires pour les accrocher et les tendre se trouvent dans des magasins pour BTP ou pour voiliers.
Quant à la membrane, n'ayant plus à subir des tensions démesurées ni à remplir simultanément toutes les fonctions ni à être monobloc, elle est relativement facile à réaliser directement sur le chantier à partir de divers produits disponibles dans les magasins de matériaux. Par exemple les membranes d'étanchéité pour toitures, dont il existe aujourd'hui des versions écologiques sans chlore ni plastifiants (voir http://sarnafil.fr ou http://www.spectraroof.com).
Si l'on souhaite réaliser un complexe multicouches pour plus de confort, on peut se tourner aussi vers les écrans de sous-toiture respirant (étanche à l'eau mais perméable à la vapeur d'eau), les isolants minces, sans parler des tissus de toutes sortes, en fibres naturelles ou synthétiques, traités ou pas.
Autre avantage d'une telle structure, il est facile de faire des ouvertures puisque la continuité de la membrane n'est plus une condition de sa résistance. De même on peut facilement inclure des parties transparentes, par exemple en fixant à l'ossature de câbles des plaques de polycarbonate qu'il n'est pas très difficile de relier à la membrane de manière étanche.
Ajoutons encore que le mode de conception et les matériaux employés n'exigent pas une précision absolue, tout écart étant rattrapable sur le chantier, ce qui facilite grandement la vie du constructeur.
biotecture
Intéressante aussi est la possibilité d'intégrer le bâtiment dans le paysage, ou plus précisément de réaliser une interaction fusionnelle de la structure avec la flore et la faune. C'est ce que Rudolf Doernach appelle la biotecture (http://www.rainforestinfo.org.au/good_wood/biotctl.htm).
Par exemple:
Des plantes peuvent pousser directement sur les mailles du filet, devenant partie intégrante de la structure à la fois dans un rôle de protection et de renfort. Je pense à une vieille serre du 19e siècle à la structure complètement rouillée qui ne tenait plus que grâce à la vigne qui avait poussé dessus.
Certaines parties du bâtiment peuvent rester en permanence ouvertes avec des arbres qui poussent entre les câbles, un ruisseau qui serpente, une petite mare, bref tout un écosystème qui est à la fois dedans et dehors.
D'autres parties du bâtiment peuvent être couvertes par une simple bâche facile à mettre et à enlever, pour réaliser selon les cas une serre, une véranda, un accumulateur de chaleur pour l'hiver, etc.
Bref, il y a de quoi expérimenter pour qui en a l'envie...