genèse et sens des formes architecturales

deuxième partie: géométries

Vahé Zartarian

© 2008

Bien que disponible gratuitement pour que tout le monde y ait accès sans barrière, ce document n'est pas pour autant sans valeur. Vous pouvez participer aux frais de création et de diffusion, en vous rendant à la page contact.

l’homme mesure de la Terre

de la terre à la Terre

La géométrie c’est, étymologiquement, la mesure de la Terre (gé en grec désigne la terre). Pas de la Terre entière évidemment, qui n’a pu être appréhendée et donc mesurée que relativement récemment, mais en premier lieu des limites du champ cultivé. C’est donc une mesure à la mesure de l’homme. Considérant aussi ce que l’on sait maintenant de l’espace, il serait plus approprié de parler d’une anthropo-géo-métrie, le terme plus limité de géo-métrie laissant croire que cette science est celle de la Terre elle-même indépendamment de qui la regarde. Cette approche qui remet l’homme au centre est aussi celle du peintre Olivier Debré lorsqu’il observe:

"C’est l’évolution des concepts qui détermine les transformations. La première structure d’espace s’est forgée durant la préhistoire. L’homme paléolithique a vécu pendant 100 000 ans dans l’informel, dans des cavernes elles-mêmes informelles. Ces populations de chasseurs suivaient les méandres de la nature. Devenus cultivateurs, ils vont tracer des sillons et les limites du champ à travailler, et ainsi structurer l’espace. Le langage créé par l’homo sapiens le forme en retour. Les mots se développent dans le lobe gauche de son cerveau. De même le concept d’espace, appréhendé par son lobe droit, devient comme la parole, son identité même. L’homme va passer ainsi à la structure géométrique.
C’est la grande révolution néolithique. L’homme néolithique a inventé les formes qui devaient durer jusqu’à nous: la droite, l’angle droit, le rectangle et, dans l’espace, le cube et le parallélépipède. La structuration de l’espace qui aboutit à la verticalité des parois et l’horizontalité des poutres est toujours en vigueur de nos jours. Nous vivons encore dans le parallélépipède rectangle néolithique…
La période historique est le développement de la structuration spatiale. Les villes antiques étaient établies selon un système d’angles et de droites. L’évolution différa suivant les régions… Les monuments de la Grèce antique révèlent la plus harmonieuse structuration. Mais l’organisation de chaque élément ne s’étend pas à l’ensemble des éléments séparés. C’est avec Rome que naît la prise de possession globale. Le rigide dessin des villes et la rectitude des voies illustrent la domination impériale. C’est le quadrillage romain. Les volumes disposés dans la nature s’imposent comme la croyance dans la réalité du monde.
Le trouble gagne l’humanité. Les divinités ne suffisaient plus à calmer l’angoisse. La foi mystique, chrétienne puis islamique, va déferler sur le bassin méditerranéen. Les villes du Moyen Age perdront le calme de la géométrie logique pour connaître les cités aux rues en dédales, compliquées comme les circonvolutions des lobes cérébraux. On abandonne le fronton triangulaire, on renonce à la coupole sensuelle pour les flèches des cathédrales, pour la verticalité des donjons. On érige des murailles dans la peur de l’ennemi mais aussi dans l’angoisse des hommes exilés sur la terre… La peinture ne recherche plus le volume. Elle s’exprime dans le plan. La juxtaposition d’échelles différentes conduit au rêve. C’est le monde des signes et des symboles. Les fondo d’oro expriment la présence vivante d’un au-delà. La foi dans l’autre monde détourne du réel. C’est la croyance dans la réalité de l’irréel.
La grande révolution importante de l’Occident après celle du néolithique et du christianisme est celle de la Renaissance… Les peintres italiens du quattrocento inventent grâce à leur génie l’espace perspectif. L’homme retrouve ses sens et regarde le monde, s’y insère et le domine. Le divin quitte le ciel de l’âme pour pénétrer la matière. L’infini s’incarne à la jonction des droites concourantes… La structuration de l’espace perspectif, qui allie la rigidité de l’angle et de la droite antique à la notion dynamique de la transformation, va devenir celle du plan des villes. L’influence de l’image du concept donné par les peintres est décisive et son application dans les organisations urbaines devient évidente… Le système perspectif a trouvé son épanouissement avec le classicisme du Grand Siècle, en France… Pendant plusieurs siècles, le plan de presque toutes les villes et capitales sera élaboré suivant ce principe. De nos jours encore, le terme d’espace évoque l’espace perspectif…
La logique quadrangulaire des villes primitives, les circonvolutions des villes du Moyen Age, les villes épanouies de l’espace perspectif, l’ennuyeux tracé du XIXe siècle, aucune formule ne correspond au présent, aux nécessité de la vie actuelle...
Nous pénétrons dans une ère nouvelle. La vitesse avec laquelle nous vivons fait directement entrer la notion de temps dans le lieu figé. Les erreurs dans l’organisation des agglomérations urbaines actuelles sont dues au manque de clarté de l’image du concept. Rien n’a remplacé en précision le système de la structuration perspectif. Cependant les peintres l’ont imaginé depuis longtemps…
L’espace à vivre doit être créé suivant l’image de la pensée actuelle dans l’épanouissement du sensible."
(Olivier Debré, espace pensé, espace créé, le signe progressif, le cherche midi éditeur 1999, p 16-21)

Avant d’en arriver comme il le suggère à appliquer à l’urbanisme et à l’architecture de nouvelles façons de se représenter l’espace, restons encore un peu avec l’approche géométrique traditionnelle pour comprendre pourquoi elle fonctionne quand même, jusqu’à quel point, et ce que l’on peut encore en tirer d’intéressant. Mais tout d’abord soulignons que cette géométrisation de l’espace n’est pas propre à l’Occident. Le champ carré et la maison carrée se retrouvent un peu partout sur la planète. En Chine par exemple. On peut encore lire dans certains idéogrammes cette construction ancienne et anthropomorphique de l’espace, comme dans des strates archéologiques:

• le champ dont la forme est tout à fait explicite,
• la maison, qui dans l’une de ses représentations s’écrit , idéogramme composé dont la signification est "carré sous un toit".

la ligne droite et ses déclinaisons

Au départ est la ligne droite. C’est-à-dire au départ de la géométrie en tant que construction abstraite parce que la ligne droite n’existe pas dans la Nature. Elle n’existe pas davantage dans les gestes de l’homme chez qui la conformation des articulations impose la circularité. Les mouvements droits exigent une très haute coordination de plusieurs mouvements rotatifs dont la maîtrise n’est pas immédiate. Mais curieusement, dans son univers de représentation, la droite prend le pas sur le cercle. Peut-être parce que le but est plus important que la manière d’y parvenir. C’est le but que l’on vise lorsqu’on se met en marche ou qu’on lance une pierre ou que l’on tend la main pour cueillir un fruit. Qu’il faille pour les atteindre faire pivoter des os les uns par rapport aux autres est secondaire. L’intention donne le sens, qui est droit. Donc au départ de la géométrie est la ligne droite. De là on passe au carré en disposant des segments identiques à angles droits, et puis du carré on passe au cube.
Du geste quotidien on passe à l’organisation spatiale du champ. De l’organisation spatiale du champ on passe à celle de la maison. De la maison on passe à la cité (cf. d’innombrables cités tant anciennes que récentes où les rues sont rectilignes et se coupent à angles droits). De la cité on passe enfin à l’état (voir des cartes de l’Amérique du Nord et de l’Afrique qui montrent de nombreuses frontières parfaitement rectilignes). On imagine facilement que, continuant sur cette lancée, les mêmes états qui ont tracé ces frontières finissent par découper la galaxie en secteurs cubiques et à se les répartir, pour le plus grand bien de toute vie évidemment…
Partout où il se pose, l’homme s’efforce d’organiser l’espace dans lequel il vit à l’image de ses représentations mentales. Comme sa pensée n’est pas assez libre, vaste et souple pour qu’il se meuve à l’aise et en conscience dans l’informel, l’indéterminé, le changeant, il projette le plus simple et le plus limité, en l’entourant, pour ne pas voir que ce sont là ses propres limites, d’une aura de vérité, d’immuabilité, d’universalité. C’est ainsi que la ligne droite est réifiée pour devenir le principal élément organisateur de l’espace. Combinée avec l’angle droit, elle se décline dans un second temps en rectangle puis dans un troisième temps en parallélépipède rectangle. Remarquons que même durant les périodes les plus mystiques où les rues se font circonvolutions qui mènent labyrinthiquement à l’église au centre de la ville, passage obligé vers le Ciel via ceux qui en ont la garde, les bâtiments restent fondés sur la ligne droite, le rectangle et le parallélépipède.
L’autre figure majeure de cette géométrie, le cercle, n’est pas aussi prégnante. Il sert à organiser l’espace lointain, inaccessible: la sphère céleste, la ronde des planètes, la rotondité de la Lune (plus tardivement celle de la Terre). Je signale là encore que ce n’est pas propre à l’Occident. Dans la symbolique chinoise par exemple, le pays est carré, comme le champ, comme la maison, tandis que l’univers est rond. En architecture l’on se sert aussi du cercle mais pour des raisons plus accessoires: décoratives (colonnes circulaires par exemple), symboliques (cf. en Chine les ouvertures circulaires dans des murs), ou techniques (le principe de l’arc qui forme voûtes et dômes est plus performant que le linteau: voir livre 1, première partie, chapitre 1). On le retrouve parfois dans des bâtiments savamment élaborés comme des églises, des monastères ou des châteaux, mais presque toujours dissimulé: l’organisation d’ensemble est à base de cercles dans lesquels le maître d’œuvre inscrit ou circonscrit des carrés, et ce sont uniquement ceux-là qui apparaissent sous forme de murs.
Expérience: regardez autour de vous et notez ce qui est droit, rectangulaire, parallélépipédique, circulaire, sphérique, et ce qui ne l’est pas. Faites la même chose en vous promenant dans la Nature. Comparez.

la géométrie euclidienne

l’espace euclidien

La géométrie est une formalisation de ces idées sur l’espace. C’est une façon de décrire l’espace extérieur et la forme des objets qu’il est supposé contenir indépendamment de leur nature. Indépendamment aussi des sujets qui le perçoivent, ici les êtres humains. Il est important de rappeler que même si ça a l’air vrai, même si un tel espace semble exister de manière indépendante, la géométrie ne décrit pas la réalité de l’espace ni de la forme des objets. Ce n’est pas non plus une représentation de l’espace à l’intérieur de notre esprit même s’il est possible d’en donner une représentation perceptible visuellement en termes spatiaux en dessinant des figures ou en réalisant des maquettes. C’est une pure abstraction conceptuelle. Qui a jamais vu dans la Nature ou qui a pu dessiner des cercles parfaits, des lignes droites infiniment minces qui s’étendent à l’infini et des lignes rigoureusement parallèles?
On appelle euclidienne cette géométrie du sens commun parce que le savant grec Euclide est le premier à l’avoir formalisée de manière rigoureuse au IIIe siècle AVJC. Il a posé un petit nombre de postulats, c’est-à-dire des principes premiers indémontrables mais allant de soi, desquels il a déduit tout le reste sous forme de théorèmes. Exemples de postulats: "par deux points donnés on peut mener une droite et une seule"; ou bien: "étant donnée une droite dans un plan, par un point extérieur à cette droite on peut mener une parallèle et une seule". Exemples de théorèmes déduits des postulats: "la somme des angles d’un triangle forme un angle plat"; ou bien: "la géométrie d’un corps rigide est conservée par translation ou rotation".
Il ne faudrait pas croire que parce que l’Occident l’a formalisée et lui a donné un nom il a le monopole de cette géométrie. Cette façon de concevoir l’espace est assez largement partagée même si elle ne fait pas l’objet de formalisations aussi savantes. Surtout, il y a en amont des postulats et théorèmes d’Euclide (gardons l’appellation consacrée même si tous ne sont pas de lui) des allants de soi encore mieux partagés, qui vont d’ailleurs tellement de soi que l’on omet souvent de les mentionner. Par exemple:

• l’espace a trois dimensions; je précise qu’il s’agit de l’espace supposé extérieur et réel, le seul qui nous intéresse en architecture, car il est évidemment possible en mathématiques de bâtir des espaces de dimensions entières quelconques;
• il est infini dans toutes les directions (c’est-à-dire en pratique jusqu’au point le plus éloigné que l’on puisse imaginer);
• il est continu et divisible;
• il est homogène c’est-à-dire que tous les points sont identiques en nature, ne se différenciant que par leur position; on peut se déplacer d’un point à un autre, ce n’est qu’un changement de position qui n’a pas d’autres incidences sur la ‘trame’ de l’espace;
• il est isotrope c’est-à-dire qu’il a les mêmes propriétés dans toutes les directions; en d’autres termes, toutes les droites passant pas un point sont équivalentes, il suffit d’une rotation pour transformer l’une en l’autre en conservant les distances.

Ceci fournit un cadre spatial censé être indépendant des objets qui s’y trouvent et des événements qui s’y déroulent. Un cadre plutôt cohérent avec notre vie quotidienne. En particulier l’homogénéité et l’isotropie assurent qu’une figure quelconque reste identique à elle-même lors d’un déplacement par translation ou rotation. En pratique bien sûr on n’a pas besoin de connaître ces mots ni leurs définitions précises pour s’en servir. C’est ainsi que l’on sait tous manier une règle pour prendre la mesure d’un objet et la transférer sur un autre. Il va de soi que la règle ne s’allonge ni ne raccourcit lors de cette opération et que c’est bien la même mesure qui est reportée. C’est donc un cadre utile qui permet de modéliser des formes et les projeter sur des objets physiques par homothétie: on dessine un patron sur une feuille de papier, on prend les mesures, on leur applique un même facteur d’agrandissement (ou de réduction), et on reconstitue la forme en plus grand (ou plus petit) sur une planche de bois, un coupon de tissu, une pierre ou tout autre support.

et pourtant, ça marche

Ce dernier exemple montre que la géométrie euclidienne, ça marche. Mais comment comprendre que justement "ça marche" si cette géométrie n’est pas une description vraie d’un espace réel, si ce n’est qu’une construction, une abstraction conceptuelle? Voici schématiquement ce qui se passe:

image intérieure => modélisation géométrique => forme construite => forme perçue

L’image intérieure que l’on forme dans son esprit, d’une maison par exemple, est déjà conditionnée par nos présupposés sur la nature de l’espace extérieur. Même si on ne les a pas continuellement en tête, les règles de la géométrie euclidienne sont présentes chez la plupart d’entre nous comme des allants de soi. On ‘sait’ qu’en se donnant deux points on pourra tracer une droite et une seule, cela va de soi, aussi bien en esprit que sur le papier que sur le terrain. On ‘sait’ qu’en reportant quatre fois ce segment de droite dans un plan en le faisant tourner à chaque fois d’un angle droit, on formera un carré, cela va de soi, que l’on soit agriculteur, charpentier, maçon, couturière, etc. On ‘sait’ qu’en multipliant toutes les dimensions d’un dessin par un même facteur et en reportant les valeurs ainsi calculées sur le terrain on obtiendra une figure similaire: un triangle restera un triangle dont tous les angles auront même valeur, un carré restera un carré, un cercle un cercle, etc. Cette homothétie est figurée par la flèche du milieu sur le schéma ci-dessus.
Mais obtient-on précisément la même chose au seul facteur d’échelle près? À vrai dire, non. Tel mur construit ne fait jamais exactement les 4 mètres de longueur spécifiés sur le plan, mais, disons, 4,03 à une certaine hauteur du sol et 3,99 à une autre. Telle ligne droite n’est pas parfaitement rectiligne, telle surface plane pas exactement plane. Pour dire que la construction est conforme au plan tracé, il faut limiter sa perception, l’orienter vers ce qui est jugé essentiel et la détourner de ce qui est jugé secondaire. Ce n’est qu’à ces conditions que le mur de pierres pourra être considéré comme plat malgré les irrégularités de sa surface, et de dimensions correctes malgré des variations de longueur et de hauteur, sans même parler des incertitudes sur les mesures.
Au final il n’est pas étonnant d’avoir l’impression que la géométrie, ça marche. On projette dans la réalité physique une forme élaborée à travers un certain filtre et ensuite on contemple la réalisation à travers le même filtre en évitant soigneusement de regarder ailleurs. Nulle surprise donc si l’image finale coïncide dans une certaine mesure avec l’image initiale.
L’erreur à ne surtout pas commettre à ce stade est de confondre succès et vérité. Ce n’est pas parce qu’elle marche, au moins jusqu’à un certain point, que la géométrie euclidienne est vraie. C’est parce qu’elle est une construction humaine employée par un être humain comme outil pour faire passer une forme de son esprit à la matière. Remarquons en passant qu’il est parfaitement possible de s’en dispenser complètement en architecture. Les constructeurs de huttes et autres habitats traditionnels simples ne s’embarrassent pas de telles complications. Ils construisent directement ce qu’ils ont en tête et en ont une perception tout aussi directe. La plupart des sculpteurs travaillent de la même manière. Tout se joue dans ce cas dans l’espace perçu sans qu’il soit besoin d’un espace intermédiaire géométrisé. Ce dernier devient en revanche nécessaire dès que l’on ne construit plus directement. Pour ce faire la géométrie euclidienne a d’indéniables qualités mais aussi quelques sérieuses limites que l’on verra le moment venu.

géométrie pratique

La géométrie des mathématiciens diffère quelque peu de celle des bâtisseurs. Pour les premiers, il est important de savoir qu’une ligne droite peut théoriquement se prolonger à l’infini tandis que pour les seconds cela ne sert à rien. Pour les premiers il est capital qu’un théorème soit rigoureusement démontré avant de s’en servir tandis que pour les seconds il suffit de le vérifier empiriquement sur quelques cas pour ne pas douter de sa validité générale.
Un petit nombre d’outils simples suffisent pour faire de la géométrie pratique. Pour dessiner: la règle, le compas et l’équerre, symboles ‘maçonniques’ s’il en est. Leur contrepartie sur le terrain: des éléments du corps en guise d’instruments de mesure (pied, pouce, pas, etc.), deux piquets et une corde pour le tracé des cercles (ainsi que des ellipses et de quelques autres figures), la corde à nœuds pour faire les angles droits. Comment fait-on un angle droit avec une corde? On prend la corde et l’on fait treize nœuds à intervalles réguliers. On tient ensemble les deux nœuds des extrémités et on forme un triangle dont les côtés font respectivement 3 unités, 4 unités et 5 unités. Le résultat est un triangle forcément rectangle parce que: 3²+4²=5² (théorème de Pythagore). C’est donc une sorte d’équerre géante pour tracer sur le terrain des angles droits. Ces instruments simples suffisent pour dessiner de nombreuses figures régulières: droites, cercles, ellipses, paraboles, rectangles, carrés, hexagones, cônes, cylindres, cubes, etc. En ajoutant un niveau et un fil à plomb on a tout ce qu’il faut pour réaliser des fondations horizontales et des murs verticaux, autrement dit pour faire des jolies boîtes parallélépipédiques. Rien d’autre n’est nécessaire pour construire des maisons, voire des châteaux et des cathédrales selon les méthodes ancestrales.

géométrie algébrique

Avant Descartes, la géométrie consistait essentiellement en tracés de figures à l’aide de ces instruments. Descartes a fait rentrer l’algèbre dans la géométrie et en a fait un instrument beaucoup plus puissant. Et beaucoup plus abstrait. En quoi cela consiste?
Pour faire simple, commençons par un plan. On se donne une origine O et deux axes perpendiculaires passant par O dénommés respectivement axe des x ou des abscisses et axe des y ou des ordonnées. Lorsqu’on représente ce plan sur un schéma, on place conventionnellement Ox horizontalement et Oy verticalement.

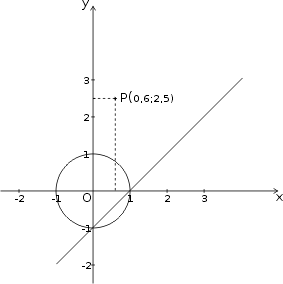
Chaque point est représenté par un couple de nombres réels (x;y) qui définissent précisément et de manière univoque sa position dans le plan. Par exemple, le point P sur la figure a pour coordonnées 0,6 selon l’axe des x et 2,5 selon l’axe des y. Donc un couple de nombres se substitue à une représentation spatiale. À partir de là toute la géométrie devient calculs mathématiques. Par exemple la distance entre deux points quelconques Q et R ne se mesure plus, elle se calcule avec la formule (dérivée de celle de Pythagore): d(P,Q)² = (Px-Qx)² + (Py-Qy)² , où (Px;Py) et (Qx;Qy) sont les coordonnées respectives de P et Q.
Dans ce plan dit cartésien une courbe n’est plus définie par son tracé mais par une équation. Par exemple:

• tous les points qui vérifient l’équation y=x-1 forment la droite inclinée à 45° qui passe par (1;0) et (0;-1);
• tous les points qui vérifient x²+y²=1 forment le cercle de centre O et de rayon 1.

Il n’est pas très difficile de montrer que dans ce cadre algébrique les règles de la géométrie euclidiennes sont vraies. Autrement dit, se donner une équation telle que x²+y²=1 est équivalent à représenter "pour de vrai" dans un plan euclidien un cercle de centre O et de rayon une unité. On voit le saut supplémentaire dans l’abstraction.

Le procédé s’étend à l’espace euclidien à trois dimensions. Il suffit de rajouter un axe Oz perpendiculaire aux deux autres. Les seules difficultés sont que les équations sont plus compliquées et les représentations graphiques moins évidentes. Voici par exemple une surface très intéressante définie par l’équation z=cxy où c est un paramètre différent de zéro. À quoi ressemble-t-elle? Impossible de l’imaginer en voyant seulement l’équation à moins d’être un mathématicien très intuitif. Je ne vous ferai pas languir, cette équation définie une selle de cheval, ou, en termes savants, un paraboloïde hyperbolique. Je vous la montrerai et vous en dirai plus dans le prochain chapitre.

La géométrie algébrique présente deux intérêts. Comme le suggère l’exemple de la selle de cheval, le premier est de permettre la construction de surfaces difficiles à concevoir autrement. Bien sûr il est toujours possible sans règle ni compas ni équerre ni équation d’aucune sorte de façonner une selle de cheval (les selliers y arrivent très bien sans recourir à aucune équation) ou la dessiner (de nombreux peintres ne s’en sont pas privés). Sauf qu’en architecture, on ne peut pas se contenter d’un dessin ou d’une maquette, aussi réalistes semblent-ils. L’architecte qui dessine une forme doit être en mesure de donner des indications précises aux charpentiers, maçons et autres corps de métiers pour qu’ils puissent la réaliser. C’est là que la géométrie algébrique pallie aux faiblesses de la géométrie traditionnelle pour permettre de passer d’une figuration à petite échelle à une construction en grandeur réelle. Remarquons encore que c’est cette même algébrisation de la géométrie qui permet l’affichage d’images sur un écran et la simulation de mouvements dans des jeux vidéos.
Son autre intérêt est de faire le lien entre la forme et la structure par le biais de théories physiques opérant dans le même cadre de représentation euclidien, comme la mécanique newtonienne. Il est ainsi possible de calculer les efforts qui s’exercent sur une forme géométrique donnée, considérée à présent comme une structure résistant à la tension et/ou à la compression et soumise à des forces.
Ceci dit, il faut reconnaître que peu de réalisations architecturales sortent de la ligne droite, du rectangle et du parallélépipède rectangle. S’agissant des formes, le vocabulaire des architectes est d’une pauvreté affligeante. Je n’ai rien contre le parallélépipède. Comme n’importe quelle forme, elle a son intérêt voire ses charmes. Le problème est qu’on ne construit pratiquement que du parallélépipède: maisons, parkings, bureaux, magasins, etc., tellement que cela n’a plus de sens. Pourtant les limites de la géométrie euclidienne ne me semblent pas atteintes. Si limites il y a dans la prolifération de la ligne droite et de ses déclinaisons bi et tridimensionnelles, c’est dans l’usage que l’on fait de l’outil, pas de l’outil lui-même. Pour preuve ce qu’il est possible de construire de radicalement différent en partant d’un simple cube.

le cube dans tous ses états

une forme peu naturelle

Il existe peu de cubes dans la Nature. Les seuls que je connaisse sont les réseaux cristallins. Encore faut-il préciser qu’un cristal qui ne serait constitué que d’un seul cube ne serait pas tout à fait un cristal. Tout cristal est déjà un assemblage de formes élémentaires qui, séparées des autres, n’ont guère d’existence. À échelle atomique il faut un peu d’imagination pour voir des cubes parce que les arêtes ne sont pas matérialisées, seuls les sommets et éventuellement les centres sont marqués par la présence d’atomes. Par chance pour nous qui ne voyons rien des atomes, il arrive que des cristaux grossissent au point de devenir visibles à l’œil nu: cf. des cristaux de banal sel de cuisine, particulièrement sous la forme de "gros sel". C’est à cette échelle que l’on peut observer des formes minérales à peu près cubiques.
Nous voilà apparemment bien loin de l’architecture. Pourtant ce pourraient être des raisons similaires qui ont conduit à la banalisation du cube, et plus généralement du parallélépipède rectangle: la possibilité d’étendre le réseau dans toutes les directions en accolant simplement des éléments identiques. D’où concrètement des bâtiments à base de modules parallélépipédiques, autrement dit des pièces, accolés les uns aux autres tant en longueur qu’en largeur qu’en hauteur. Le cube a une énorme propension à la grégarité, au contraire de la sphère qui est un objet solitaire et ne s’assemble avec d’autres qu’avec difficultés et au risque de perdre son identité. Comparez une bulle de savon solitaire de forme à peu près sphérique à de la mousse savonneuse où les bulles laissent place à divers polygones et polyèdres.
Peu de cubes dans la Nature mais énormément dans l’environnement humain depuis la révolution géométrique amorcée au néolithique. Il est devenu tellement banal que c’est à se demander s’il y a encore quelque chose à en tirer. D’expérience je peux dire que oui, mais pour ça il faut se creuser un peu la tête, voire un peu beaucoup pour ceux qui ont du mal à se représenter des surfaces courbe dans l’espace tridimensionnel. Le mieux pour sortir de cette banalité est de tenter une approche de biais.

partition du cube

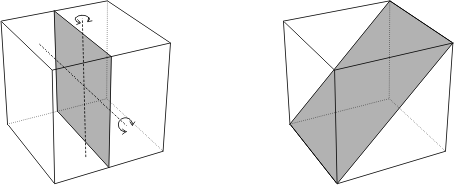
Question: trouver différentes manières de partager un cube en deux parties égales par une surface continue. Deux solutions se présentent immédiatement à l’esprit:

En y regardant de plus près, on remarque que la seconde dérive de la première par rotation du plan de coupe autour d’un axe médian horizontal. D’ailleurs on peut construire toute une famille de solutions par rotation continue de ce plan autour d’un axe médian horizontal ou vertical (en pointillés sur la première figure).
À partir de là on peut créer plein d’autres familles de solutions en faisant onduler la surface de diverses manières, par exemple:

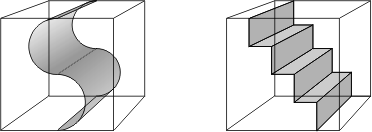
Pouvez-vous imaginer d’autres solutions? Difficile! Vous avez beau tourner et retourner le cube dans tous les sens, vous ne voyez pas. Ne vous en voulez pas car on arrive maintenant à des surfaces doublement courbées qui nous sont peu familières et pas faciles à se représenter quand on n’a pas l’objet devant soi:

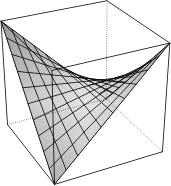
Comme annoncé, revoici la selle de cheval, ou paraboloïde hyperbolique. Pour les maniaques c’est même plus précisément un paraboloïde hyperbolique équilatère.

le paraboloïde hyperbolique

Les mêmes maniaques seront contents d’apprendre que pour un cube de côté L, l’équation du paraboloïde hyperbolique équilatère inscrit dans les diagonales des faces s’écrit, en plaçant l’origine au centre du cube:

Oublions la démonstration et bornons-nous à constater que cette formule a toutes les symétries requises pour bien partager le cube en deux. Précision importante, la surface ne s’arrête pas aux frontières du cube mais se prolonge à l’infini dans toutes les directions.
Ce paraboloïde hyperbolique équilatère est un cas particulier d’une surface plus générale définie par l’équation:

Elle est appelée paraboloïde parce que certaines sections de cette surface par des plans sont des paraboles. Il s’agit précisément de toutes les sections par des plans verticaux X=constante ou Y=constante. Les sections par des plans z=constante sont quant à elles des hyperboles, d’où le qualificatif d’hyperbolique (par opposition à une autre famille de paraboloïdes définie par une équation du second degré du même genre où le signe - est remplacée par le signe +, auquel cas certaines sections deviennent des ellipses au lieu d’hyperboles, d’où leur nom de paraboloïdes elliptiques, mais c’est une autre histoire…). En voici une représentation qui fait apparaître les différentes familles de paraboles et d’hyperboles:

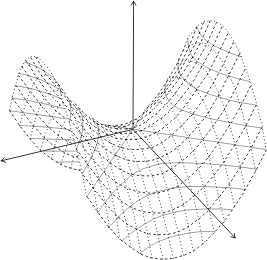
Si a=b le paraboloïde hyperbolique devient équilatère. Les lecteurs attentifs n’auront pas manquer de remarquer que les deux équations ne se ressemblent pas du tout. Pourtant il s’agit bien de la même. Miracle des mathématiques, on passe de l’une à l’autre en faisant tourner le repère XOY de 45° par rapport à xOy selon l’axe Oz qui reste inchangé.

morphogenèse du paraboloïde hyperbolique

Il y a plusieurs manières d’engendrer une telle surface. La première se déduit aisément de l’équation générale. Elle consiste à faire glisser une parabole z=-Y²/b² le long d’une autre parabole inversée et située dans le plan perpendiculaire z=X²/a² (ou bien l’inverse, faire glisser la seconde parabole sur la première):

remarque:il s’agit d’un gif animé, si l’animation ne marche pas, essayez de recharger la page en cliquant sur le bouton actualiser, sinon vérifiez les options de votre navigateur (dans Explorer: outils > options internet > avancé > multimedia > lire les animations dans les pages web)

Engendrer un paraboloïde hyperbolique comme surface de translation n’a d’intérêt que d’un point de vue géométrique. Je n’en vois aucun du point de vue architectural étant donnée la difficulté déjà de réaliser une simple parabole, que ce soit en dur (pierre, béton, etc.) ou en courbant des matériaux souples (bambou, tubes de fibre de verre, etc.).

Il existe un autre procédé plus opérationnel quoique beaucoup plus difficile à découvrir. Je ne vous ferai pas languir et vais vous dévoiler sans tarder le secret: le paraboloïde hyperbolique est une surface réglée. Nous voilà bien avancés n’est-ce pas? En fait cela veut simplement dire qu’il est une réunion de droites.

remarque:il s’agit d’un gif animé, si l’animation ne marche pas, essayez de recharger la page en cliquant sur le bouton actualiser, sinon vérifiez les options de votre navigateur (dans Explorer: outils > options internet > avancé > multimedia > lire les animations dans les pages web)

Passons sur la démonstration et contentons-nous de la conclusion: un paraboloïde hyperbolique peut être engendré par le déplacement d’une droite s’appuyant sur deux droites fixes non coplanaires (c’est-à-dire qui ne sont pas situées dans un même plan). Qui se serait douté que ces deux animations produiraient la même surface? C’est tout l’intérêt des mathématiques. Et c’est quasi miraculeux qu’en tripotant ces équations on parvienne à une solution aussi simple à réaliser. Par exemple:

Remarques: sur la première photo on voit bien les lignes droites, et sur la seconde on devine la double courbure. Cette réalisation présente en outre la particularité d’être autoportante c’est-à-dire qu’elle n’a besoin d’aucun ancrage pour tenir.

Autre manière concrète de réaliser une portion de paraboloïde hyperbolique: on accroche des élastiques à intervalles réguliers entre deux tiges rectilignes, puis on écarte les tiges en donnant un mouvement de rotation pour les rendre non coplanaires.

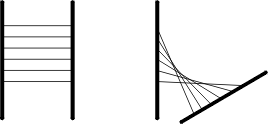
Pour résumer, cette surface d’apparence très complexe se révèle finalement assez facile à construire à partir simplement de lignes droites. Cela ouvre d’intéressantes perspectives en architecture puisque les matériaux les plus courants sont rectilignes. En précisant qu’il ne s’agit pas de mettre du paraboloïde hyperbolique partout mais seulement de suggérer qu’il existe des alternatives au parallélépipède pas beaucoup plus difficiles à réaliser.

parenthèse sur la sphère

Nous avons donc trouvé un moyen simple de créer une surface dont la double courbure tranche avec la platitude à laquelle nous sommes trop souvent confrontés et à laquelle nous nous sommes hélas habitués. Et pour ce faire rien de bien compliqué, il suffit de mener des lignes droites entre deux droites fixes non coplanaires. Étonnant non?

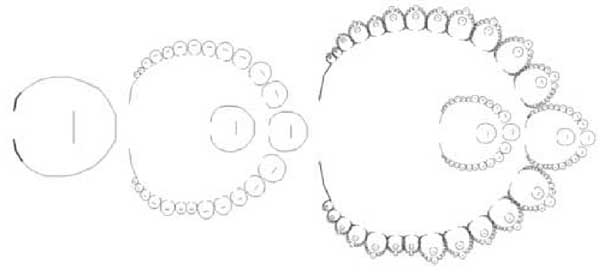
Avant de poursuivre avec nos jeux de cubes, demandons-nous si nous aurions pu jouer le même jeu avec la sphère, autre figure euclidienne ‘universelle’. En fait cela a déjà été fait dans le livre 1, deuxième partie. Par une toute autre voie nous sommes parvenus à un résultat également remarquable, rien moins qu’un procédé révolutionnaire de construction de la sphère. Pour ce faire nous avons combiné celle-ci avec des polyèdres réguliers inscrits, en particulier l’icosaèdre formé de 20 triangles équilatéraux identiques. C’est ainsi qu’une pure question de géométrie a débouché sur un principe structural très élégant et d’une remarquable efficacité. Il s’agit du dôme géodésique que l’on doit à Buckminster Fuller dans les années 1950.

Preuve est faite, la géométrie euclidienne n’a pas encore tout donné. Il faut juste la bousculer un peu pour sortir des banalités habituelles. De figures géométriques aussi simples que la sphère et le cube on est parvenu à tirer non seulement de nouvelles formes mais aussi de nouveaux procédés constructifs. Imaginez l’enrichissement du vocabulaire des formes architecturales si l’on bousculait de même polygones et polyèdres divers, cônes, cylindres, etc. Je ne poursuivrai pas plus avant dans cette voie, l’important était surtout de montrer que c’est possible. Pour les amateurs j’ajouterai que C.E. Henderson a fait de son côté le même genre de travail sur le cône jusqu’à proposer un nouvel habitat très original tant du point de vue de la forme que du procédé constructif: http://fishrock.com/conics. Revenons maintenant au cube, nous n’en avons pas encore tout à fait fini avec lui.

jeux de cubes

L’un des intérêts du cube (et plus généralement du parallélépipède) est la grande facilité qu’il a à s’assembler avec lui-même. Le paraboloïde hyperbolique équilatère réduit à la portion inscrite dans un cube hérite bien évidemment de cette propriété (c’est possible aussi s’il est inscrit dans un parallélépipède). Il y a juste une condition supplémentaire si l’on veut réaliser une surface continue: faire coïncider d’un cube à un autre les bordures des portions de paraboloïdes hyperboliques. Ce n’est pas très difficile vu que les lignes en question sont des droites et même plus précisément des diagonales des faces:

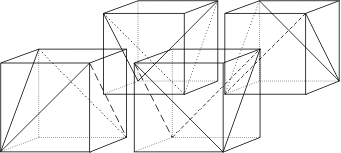
Voici une variante en voile de béton pour une salle de spectacle due à Milo Ketchum:

http://www.ketchum.org

Le toit est formé de quatre portions identiques de paraboloïdes hyperboliques. Il fait environ 60 mètres de côté. L’épaisseur est de 75 mm seulement, hormis les nervures qui sont un peu plus épaisses.
D’accord, ce n’est pas la huitième merveille du monde. Le paraboloïde hyperbolique a été employé dans d’autres circonstances avec plus d’élégance. Si j’ai tout de même choisi cet exemple c’est qu’il laisse bien deviner l’assemblage des quatre portions. Et puis il suggère qu’il n’y a pas de fatalité, que l’on peut échapper à la platitude, mettre quelques rondeurs sans choquer personne ni compliquer exagérément la construction.
Voici une proposition personnelle un peu plus originale, à l’état de maquette seulement:

Abandonnons le paraboloïde hyperbolique mais continuons avec nos jeux de cubes. Jusqu’ici nous n’avons travaillé qu’avec un seul et n’avons réalisé des assemblages que dans un second temps. Inversons la démarche et partons maintenant d’un assemblage de cubes. En voici un peu ordinaire mais pas très compliqué alternant pleins et vides:

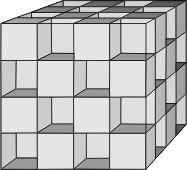
À quoi ça peut servir? Pas à grand chose sinon à suggérer une manière étonnante de partager l’espace en deux sous-espaces absolument identiques qui ne peuvent pas communiquer. Vous ne voyez pas? même si je vous dit qu’ils se déduisent l’un de l’autre par une simple petite translation? même si je rajoute de ne plus vous prendre la tête avec des surfaces courbes? Alors voici:

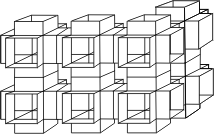
Et voici le bloc de base qui par assemblage permet de construire la surface de séparation entre ces deux sous-espaces:

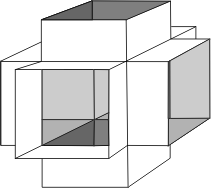
Regardez bien et vous comprendrez que les deux sous-espaces ne communiquent jamais, sauf à faire un trou dans la surface de démarcation. Les deux s’étendent à l’infini dans toutes les directions, les deux sont identiques et se déduisent l’un de l’autre par translation, les deux cohabitent dans le même espace, mais on ne peut pas dire que l’un soit le dehors de l’autre parce que, d’un strict point de vue géométrique, ils ne communiquent pas. Ce sont plutôt des univers parallèles.

Sommes-nous si loin de l’architecture? Pas tant que cela à vrai dire. Souvenez-vous par exemple de ces anciennes maisons de maîtres: dans le même bâtiment il y avait des pièces, des couloirs, des entrées, des escaliers réservés à la domesticité, et d’autres pièces, d’autres couloirs, entrées et escaliers réservés aux maîtres, les deux espaces ne communiquant que par quelques portes discrètes et à certains moments bien précis de la journée. Deux sous-espaces parallèles imbriqués dans le volume du même bâtiment. À quand des immeubles sur le même principe réalisant un parfait apartheid tout en donnant l’illusion d’une mixité sociale?

passage dedans-dehors

L’exemple précédent commence à nous faire rentrer dans des espaces un peu bizarres. Le cadre général reste euclidien mais certains repères s’estompent comme la traditionnelle séparation dedans-dehors. Comme justement une bonne partie du travail de l’architecte consiste à élaborer une telle séparation, il est intéressant de poursuivre cette exploration d’objets géométriques un peu particuliers. Commençons par un exemple tout simple et assez connu appelé ruban de Möbius, du nom du mathématicien et astronome allemand du 19e siècle qui le premier en a étudié les propriétés topologiques.

le ruban de Möbius

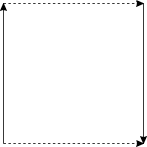
Découpez deux bandes de papier. Prenez la première et reliez les deux extrémités pour faire un ruban classique comme ceci:

Prenez la seconde bande et reliez les extrémités après avoir effectué une torsion d’un demi-tour de sorte que A n’est plus en vis-à-vis de C mais de D, et B de C:

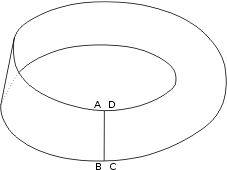
A priori il ne semble pas y avoir de grandes différences entre ces deux objets géométriques. Et pourtant: le premier a deux bords et deux côtés tandis que le second n’a qu’un seul bord et qu’un seul côté! Bizarre mais facile à vérifier:
Prenez un feutre et colorez le bord du ruban classique. Une fois revenue au point de départ, vous constatez qu’un bord est coloré et l’autre pas. Faites la même chose avec le ruban de Möbius. Une fois revenue au point de départ, vous constatez cette fois que tout le bord est coloré.
Reprenez le ruban classique et tracez une ligne au milieu. Votre ligne refermée, vous constatez qu’un côté du ruban reste vierge. Faites la même chose avec le ruban de Möbius. Vous constatez cette fois que la ligne passe partout: il n’y a qu’un seul côté.
Question subsidiaire: pouvez-vous prévoir ce qui va se passer si vous coupez le ruban de Möbius avec des ciseaux le long de la ligne médiane que vous venez de tracer? Je vous laisse faire l’expérience. Étonnant non?

Le ruban de Möbius n’est pas qu’un casse-tête pour géomètres et on lui trouve des applications pratiques. Par exemple des courroies de convoyage ou de transmission. Comme elles n’ont qu’un seul côté, l’usure est plus régulière et elles durent plus longtemps.
En architecture je ne lui vois guère d’applications parce que j’imagine mal comment délimiter un volume intéressant avec une telle surface. On trouvera probablement plus d’inspiration dans une surface plus compliquée et encore plus bizarre dérivée de la précédente. Il s’agit de la ‘bouteille’ de Klein, du nom d’un autre mathématicien allemand du 19e siècle.

la bouteille de Klein

Cet objet géométrique est une extension du ruban de Möbius dans une dimension supplémentaire. Voici une manière de le concevoir:

On part d’une surface carrée. On identifie le bord du haut et le bord du bas. Puis on identifie le bord droit avec le bord gauche après avoir effectué une rotation d’un demi-tour comme dans un ruban de Möbius. Comme l’objet résultant de cette opération doit passer à travers lui-même, il n’existe en pleine intégrité que dans un espace à 4 dimensions. On peut néanmoins l’immerger dans notre espace à 3 dimensions mais cela fait apparaître une sorte de trou, comme un goulot, d’où le nom de ‘bouteille’ de Klein.

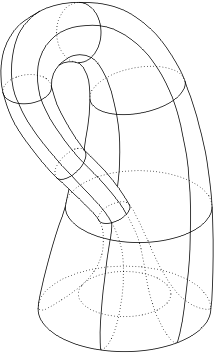
Attention, ce n’est une ‘bouteille’ que par grossière analogie parce que contrairement à une bouteille classique cet objet n’a pas de ‘goulot’ à proprement parler. Un peu comme une surface sphérique il n’a pas de bord: on peut se promener dessus sans jamais être arrêté. Mais à la différence de la sphère et à l’analogue du ruban de Möbius, cette surface a un seul côté et non pas deux. Une mouche peut marcher dessus et se retrouver indifféremment dedans ou dehors sans avoir à passer à travers la surface ni franchir de bord. En fait cela signifie qu’il n’y a pas vraiment de dedans ni de dehors.

Dans l’architecture occidentale, les notions de dedans et de dehors ont un sens très fort et le passage de l’un à l’autre est véritablement conçu comme une frontière. Conception qui n’est pas prête de changer quand on voit ce qu’on nous prépare: des maisons super isolées comme des bouteilles thermos, présentées comme la seule réponse possible à la crise énergétique et au réchauffement climatique. C’est sûr, cela va faire vendre des kilomètres cubes de laine de verre. Il est moins sûr que le confort et la santé des habitants y gagnent. Dans le livre 3 je propose une autre piste, juste histoire de montrer qu’on a le droit et la possibilité de ne pas se laisser enfermer dans des conceptions élaborées encore une fois sans véritable considération de la vie en générale et de l’être humain en particulier. D’ailleurs le mot ‘isolation’ dit bien ce qu’il veut dire…
En attendant remarquons que les japonais ont une tout autre conception du dedans et du dehors. Pour eux les deux ne s’opposent pas. C’est fondamentalement la même chose et l’on passe continûment d’un espace lointain et sauvage, c’est-à-dire sans la moindre présence humaine ou à peine, à un espace intérieur qui n’est rien d’autre qu’un espace naturel mais plus ordonné, plus maîtrisé selon des critères humains. Notons le caractère intermédiaire du jardin japonais (et avant lui chinois) puisqu’il est un bout de nature d’apparence sauvage sur lequel la maison ouvre largement tout en étant entièrement fait de main d’homme. Dans une maison japonaise traditionnelle, il y a donc une succession d’espaces de transition et non pas une frontière nette et quasi étanche entre ce qui est considéré comme dedans et ce qui est considéré comme dehors.
Qu’on n’aille pas en tirer la conclusion qu’une telle maison est une sorte de bouteille de Klein. Je ne crois pas non plus qu’une maison ressemblant à une bouteille de Klein soit désirable. Je veux juste montrer que cet objet géométrique peut stimuler notre imagination, que ses propriétés comme l’absence de bord et de séparation dedans-dehors qui nous apparaissent bizarres peuvent nous aider à dépasser certaines limitations que nous nous imposons sans nous en rendre compte. De ces cogitations sortiront peut-être des formes architecturales intéressantes. Je n’en sais rien. Je suis sûr en revanche que l’architecture doit repenser la question du dedans-dehors. J’y reviendrai dans le livre 3.

On sent qu’on s’est considérablement éloigné des banals cubes et autres sphères de la géométrie euclidienne classique, tout en restant dans l’architecture. Je propose de nous en éloigner encore davantage pour rentrer dans un tout autre univers, celui de la géométrie fractale.

géométrie fractale

origines

Même si sa naissance officielle date du début des années 1970 seulement, les origines de la géométrie fractale remontent plus avant dans le 19e siècle. Elle est née d’un certain nombre de constats, découvertes, interrogations. Suivons quelques uns de ces développement, c’est probablement la meilleure manière de prendre pied dans cet univers peu familier.

irrégularité des formes naturelles

Dans la géométrie euclidienne, l’espace est parfaitement régulier, c’est-à-dire continu, homogène, isotrope. Les formes qui s’y déploient étant conçues comme simple partition de cet espace, elles possèdent la même régularité: la ligne droite, le cercle, le carré, le triangle, la sphère, le cube, le cône, etc., plus toutes les déformations continues que l’on peut opérer sur elles telles que trous, torsions, aplatissements, etc. L’irrégulier et le discontinu sont hors de portée des outils de la géométrie euclidienne. Quand ils surgissent inopinément au détour d’une équation, on s’empresse de les qualifier de "points singuliers", façon de les mettre de côté en soulignant leur anormalité.
Or force est de constater qu’un très grand nombre de formes naturelles ne répondent pas à ces critères. Observez l’eau courante, les reflets dans l’eau, les arbres et leur écorce, les flocons de neige, les rochers et les montagnes, les flammes et la fumée, les nuages, etc. Impossible de ramener ces formes à des ronds, des carrés, des triangles, ni à des sphères, des cubes, des cônes, ni à des surfaces ou des volumes qui en dériveraient par toutes sortes de déformations. Bref, la plupart des formes que nous percevons dans la Nature ont un degré d’irrégularité tel que la géométrie euclidienne devient totalement inopérante.
Remarquons que si nous n’avons aucun mal à percevoir et à reconnaître ces formes c’est bien que notre espace de représentation n’est pas limité par le cadre euclidien. Cela sous-entend également que la genèse de ces objets se fait nécessairement en-dehors d’une représentation euclidienne de l’espace. Question: peut-on tout de même modéliser ces objets?

des lignes aux surfaces et des surfaces aux volumes

On a appris qu’une ligne est un objet géométrique de dimension 1, une surface de dimension 2, et un volume de dimension 3. La dimension est reliée simplement au nombre de coordonnées nécessaires pour se repérer sans ambiguïté sur l’objet en question. Sur une route par exemple, qui est assimilable à une ligne continue, une seule coordonnée suffit pour savoir précisément où l’on se trouve, le kilométrage depuis l’origine. Sur une carte d’un pays, il faut deux coordonnées pour localiser une ville, la longitude et la latitude. Et dans l’espace aérien il faut ajouter une troisième coordonnée, l’altitude. Tout cela va de soi et il n’y a rien à redire.
Quoique! Lorsqu’on regarde de près certains objets naturels on est contraint de s’interroger sur cette notion de dimension. Il arrive en effet qu’on ne sache plus trop si l’on a affaire à des lignes ou des surfaces, à des surfaces ou des volumes. Considérons par exemple un poumon. En gros c’est une sorte de sac rempli d’air. Il a à peu près la même contenance que ces petits sacs plastiques que l’on distribue dans les magasins. Si vous découpez et étalez bien à plat la membrane d’un tel sac, vous constaterez que sa superficie n’est pas très grande, guère plus d’une dizaine de décimètres carrés. Partant il est raisonnable de penser que la superficie du poumon ne doit pas être très différente. Eh bien pas du tout: si l’on pouvait complètement l’étaler sans la déchirer, la surface de contact avec l’air se révèlerait plus étendue qu’un court de tennis. Mais dans notre corps elle est tellement convolutée (et non pas repliée comme une feuille de papier car tous les points doivent être en contact avec l’air) qu’elle tient dans les quelques litres du poumon. C’est une surface certes, mais qui est davantage assimilable à un volume.
Peut-on donner une assise mathématique à ce genre d’observation? On doit au mathématicien italien Peano (1858-1932) la découverte en 1890 d’une très étrange courbe qui porte son nom. Voici comment elle est construite:
Première étape. On part d’un carré d’une unité de côté qu’on partage en 9 carrés plus petits. On construit ensuite un chemin qui passe successivement par tous les carrés, sans se recouper. Parmi plusieurs chemins possibles, en voici un:

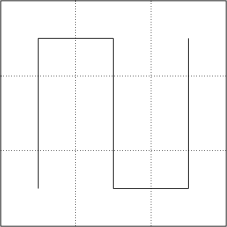
Deuxième étape. Chacun des 9 carrés est traité comme le grand carré initial c’est-à-dire qu’il est à son tour divisé en 9 carrés plus petits et le motif de base est reproduit. En alternance le motif est inversé pour pouvoir construire un chemin continu et ne se recoupant pas qui passe successivement par les 81 petits carrés:

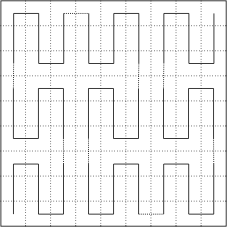
L’opération est renouvelée:

Répété à l’infini, le processus permet d’obtenir une ligne continue qui remplit entièrement le carré. Attention, il ne s’agit pas comme dans du tissage, du tressage, du tricotage ou de la broderie de construire une surface avec une ligne d’une certaine épaisseur, même si elle est aussi fine qu’un fil de soie. Ici la ligne est un objet mathématique dépourvu d’épaisseur. La courbe de Peano est un objet unidimensionnel (une ligne sans épaisseur) qui recouvre entièrement une surface bidimensionnelle (le carré). Le procédé peut être étendu pour remplir de la même manière un volume.
De la ligne à la surface et de la surface au volume, les frontières ont l’air de se dissoudre. Au fond, nous ne devrions pas être surpris puisque nous savons que ces notions ne sont que des abstractions et pas la réalité. Elles naissent de notre manière de regarder les formes. Nous pouvons construire des géométries où elles ont un sens, comme la géométrie euclidienne. De fait, si l’on assimile la surface de la planète à une surface euclidienne, alors on peut effectivement se repérer dessus avec deux coordonnées, on peut sans difficulté mesurer la distance entre deux localités, etc. Mais ce n’est qu’une manière de regarder. Il y en a d’autres à partir desquelles nous pouvons construire d’autres géométries dans lesquelles ces notions n’ont plus de sens, ou plus le même sens. Des géométries où, par exemple, il est impossible de s’accorder sur une mesure unique de la distance entre deux localités.

la longueur de la côte bretonne

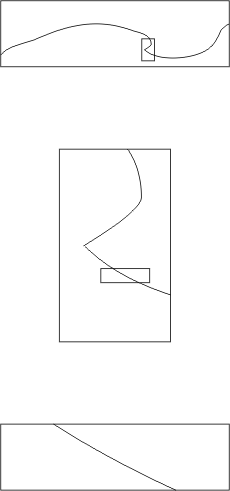
Le facteur qui a déclenché la découverte des fractales par Benoît Mandelbrot (1924-) a été cette question d’apparence toute bête: quelle est la longueur de la côte bretonne?

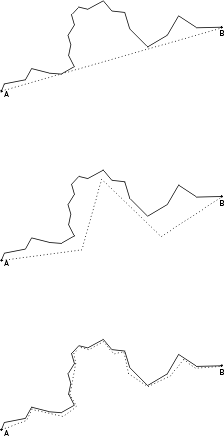
Si je survole cette côte en avion, je vais parcourir en ligne droite 3 unités de longueur pour relier le point A au point B (dessin du haut). Si je prends la route qui longe la côte, quelques inévitables virages vont porter la distance parcourue à 4 unités (dessin du milieu). Si maintenant je marche le long des falaises et des plages, je vais encore me rallonger en suivant tous les contours du rivage, d’où une distance parcourue encore plus grande de 5 unités (dessin d’en bas).
Rien de bouleversant jusque là. Mais si l’on pousse plus loin la réflexion sur la notion même de mesure, on en arrive à ceci: la longueur d’une ligne irrégulière dépend de l’étalon de mesure. Autrement dit, plus l’étalon de mesure diminue (ici une longueur mais le raisonnement s’applique pareillement à des surfaces et des volumes), plus la taille de l’objet augmente. En fin de compte la côte bretonne n’a pas de longueur dans l’absolu, elle n’en a une que dans le cadre d’une opération de mesure à l’aide d’un instrument de mesure parfaitement spécifié.
Ceci est contraire au ‘bon’ sens qui incline à penser que l’objet possède en soi une ‘vraie’ longueur, laquelle doit finir par se dévoiler comme convergence d’un faisceau de mesures. Ce serait le cas si l’objet était régulier, une jolie courbe bien formée comme toutes celles que l’on étudie en géométrie euclidienne. C’est d’ailleurs par une méthode de ce genre que l’on a pu approcher le périmètre d’un cercle et obtenir les premières approximations de pi: en additionnant des segments de plus en plus petits mais de plus en plus nombreux de polygones réguliers inscrits dans le cercle, la mesure converge sur le périmètre du cercle. Sauf que le procédé ne marche plus du tout lorsqu’on a affaire à des objets qui restent irréguliers à toutes les échelles. Alors la longueur devient infinie lorsque l’unité de mesure tend vers zéro.

quelques caractéristiques de la géométrie fractale

Le but de ce chapitre n’est pas de faire un cours complet et rigoureux sur le sujet mais seulement de donner un aperçu de ses principes pour voir ce que l’on peut en tirer d’utile pour l’architecture. Dans ces conditions le mieux me semble de procéder à une comparaison point à point avec ce que l’on connaît mieux, la géométrie euclidienne.

algorithmes vs. équations

Les objets euclidiens sont décrits par des opérations géométriques simples ou par des équations. On en a vues quelques exemples plus haut qui définissent des lignes et des surfaces. Ce qu’il importe de souligner ici c’est que ces procédés donnent d’emblée la position dans l’espace de tous les points de l’objet.
Les objets fractals sont quant à eux définis par des algorithmes itératifs. Il s’agit de procédures qui répétées et répétées et répétées encore à l’infini donnent naissance aux dits objets. On a vu un tel processus à l’œuvre pour engendrer la courbe de Peano. Voici un autre exemple plus séduisant et plus connu, la courbe de Koch.
Il s’agit d’une courbe continue, sans tangente, obtenue par une construction géométrique très simple. On part d’une ligne droite que l’on divise en trois segments égaux. On fait subir une rotation de 60 degrés à celui du milieu et on en rajoute un autre de même longueur pour reformer une ligne continue. On répète l’opération pour chacun des quatre segments ainsi obtenus. Et ainsi de suite…

En réunissant en triangle trois éléments de ce genre on obtient une jolie figure qui ressemble à un flocon, d’où son nom "flocon de Koch".

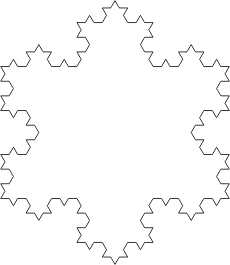
facteur dimensionnel

Remarquons que le plan dans lequel se développent la courbe et le flocon de Koch est le plan euclidien que l’on connaît. En revanche ces objets n’ont plus du tout les caractéristiques de formes euclidiennes. Par exemple l’on ne sait plus trop si l’on affaire à une ligne ou une surface.
Reprenons le flocon de Koch. À l’étape de construction d’ordre n, on a 3x4ⁿ segments ayant chacun une longueur de 1/3ⁿ si l’on prend le segment de départ égal à 1. D’où une longueur totale de 3x(4/3)ⁿ. On remarque facilement (parce que 4/3>1) que ce nombre tend vers l’infini lorsque n tend vers l’infini. Je vous épargnerai les calculs mais on peut montrer que la surface du flocon de Koch tend elle vers 0,4x3^1/2. Voici donc un objet qui a un périmètre infini mais une aire finie. Bizarre pour une forme qui ressemble quand même un peu à un hexagone ou un dodécagone. C’est comme si l’on vous disait qu’à partir de maintenant un hexagone d’une aire donnée a une circonférence infinie. Un tel objet est tout bonnement inconcevable en géométrie euclidienne. Et pourtant il existe, on vient de le construire.
On ne peut concevoir une telle figure où une ligne infinie entoure une surface finie qu’en se représentant un bord d’une certaine épaisseur. C’est ainsi qu’en géométrie fractale l’on n’a plus affaire à des lignes ni à des surfaces ni à des volumes à proprement parler mais à des objets géométriques intermédiaires, possédant de ce fait une dimension fractionnaire et non plus entière. De là d’ailleurs leur nom puisque fractal vient de fractionnaire. Ajoutons que pour compliquer encore les choses il n’existe pas de manière unique de calculer cette dimension, mais passons. Exemple: une modélisation fractale des poumons conduit à leur attribuer une dimension non entière de 2,9 qui est plus proche d’un volume (dimension 3) que d’une surface (dimension 2).

facteur d’échelle

Autre bizarrerie: si l’on se place sur un point qui a l’air situé sur le bord du flocon, il est difficile de savoir s’il appartient effectivement au flocon ou s’il est en-dehors tant la forme est irrégulière. Là encore la différence est notable avec les formes euclidiennes où l’on sait toujours précisément où l’on se trouve, sur la forme ou en dehors.
En fait, plus on regarde à fort grossissement un objet géométrique régulier, aussi complexe soit-il en apparence, plus il se simplifie jusqu’à se confondre avec la droite tangente dans le cas d’une ligne ou le plan tangent dans le cas d’une surface.

Au contraire, effectuer un zoom sur un objet fractal ne change rien à sa complexité. Voici ce que donne la même opération effectuée sur la courbe de Koch.

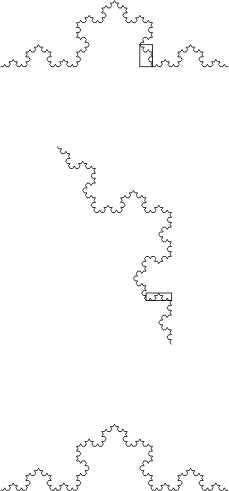
Ce qui frappe c’est non seulement que l’objet ne se simplifie pas mais qu’il reste similaire à lui-même. Cela provient du processus de formation qui est itératif. Remarquons que de nombreux phénomènes naturels peuvent être ainsi modélisés: tourbillons d’air ou d’eau, paysages, croissances des arbres, etc. Mais remarquons aussi que tous les objets fractals n’ont pas nécessairement cette propriété d’autosimilarité. Quelques uns présentent même des seuils à certains échelles où ils changent subitement de forme sans pour autant se simplifier. Si l’on prend un arbre par exemple, le processus de création et de croissance des branches est effectivement autosimilaire. Mais arrive un seuil où ce ne sont plus des branches qui poussent mais des feuilles, elles aussi modélisables par un algorithme fractal.

applications

La géométrie fractale s’avère très efficace pour modéliser de nombreux objets naturels: des paysages, les poumons, les intestins, le réseau sanguin, toutes sortes de plantes, des arbres aux fougères en passant par des herbes. Un exemple:

David Green (http://www.csu.edu.au/dgg.html) a trouvé un algorithme algébrique (ceux qu’on a vus jusqu’ici étaient purement géométriques) qui permet de fabriquer un objet fractal dont la représentation dans le plan ressemble à une fougère. Je ne sais pas comment il a réussi à le concevoir tant c’est à la fois simple et bizarre. Il s’agit de calculer successivement les coordonnées des points qui constituent l’objet à l’aide des équations suivantes:

X(n+1) = aXn + bYn 
Y(n+1) = cXn+ dYn + e

où l’ensemble des paramètres (a,b,c,d,e) prend des valeurs différentes selon certaines probabilités:

Partant d’un point de départ donné (X0;Y0), par exemple (0;1), on construit (X1;Y1) à l’aide d’une des quatre transformations, laquelle est sélectionnée en fonction de sa probabilité grâce à un tirage aléatoire. À partir de là on construit le point suivant en procédant à une nouvelle sélection de la transformation à utiliser grâce à un nouveau tirage aléatoire. Et ainsi de suite. J’ai programmé cet algorithme dans un tableur et effectué 5000 itérations. S’il avait fallu faire ça à la main… Je ne parle même pas de tester toutes sortes de valeurs des paramètres pour seulement voir si cela donne quelque chose d’intéressant. La géométrie fractale est difficilement praticable sans ordinateur. Et non content d’avoir effectué tous les calculs, l’ordinateur a aussi gentiment disposé tous les points dans un joli graphique:

Ça ressemble effectivement à une fougère même si l’on a beaucoup de mal à imaginer un lien entre les équations ci-dessus et une vraie fougère. Il n’y en a sans doute aucun mais force est de reconnaître que "ça marche", c’est étonnamment ressemblant. En se triturant la cervelle on arrive à construire ainsi toutes sortes d’algorithmes pour simuler des plantes, des paysages, des pilosités, etc., autant en deux qu’en trois dimensions. On comprend pourquoi ils sont de plus en plus utilisés pour créer des scènes réalistes dans des jeux vidéos, des logiciels de simulations et autres films d’animation.
Je m’empresse de préciser que si la géométrie fractale se révèle bien plus apte que la géométrie euclidienne à rendre compte des formes de nombreux objets naturels, elle n’est pas ‘vraie’ pour autant. Encore une fois ne confondons pas succès et vérité. Il n’existe pas plus de vrais objets fractals dans la Nature qu’il n’existe de vrais ronds ou de vrais carrés. La ressemblance entre le dessin ci-dessus et une vraie fougère provient entièrement de notre regard. D’abord parce qu’une fougère se déploie dans un espace tridimensionnel et pas seulement en plan. Ensuite elle ne naît pas d’un saupoudrage de points sans liens entre eux mais par ontogenèse à partir d’une cellule initiale qui se divise un très grand nombre de fois. Finalement, comme n’importe quelle géométrie, la géométrie fractale se révèle n’être qu’une abstraction. Et encore une fois, cela ne lui ôte pas son utilité, cela fixe juste ses limites.

géométrie fractale et architecture

Et en architecture? On a trouvé en Afrique des villages agencés selon une procédure itérative, par exemple ce village Ba-ila en Zambie:

american geographic institute dans Pour la science N°256, février 1999

Le motif initial (à gauche) est répété en plus petit sur les segments qui le compose puis répété à nouveau:

dans Pour la science N°256, février 1999

Cet exemple relève plus de l’urbanisme que de l’architecture. À ma connaissance aucun bâtiment n’a encore été conçu à l’aide des règles de la géométrie fractale. Je pense que cela tient davantage à l’ignorance et à l’habitude de travailler avec la géométrie euclidienne qu’à une limitation intrinsèque de ce nouvel outil. Peut-être aussi parce qu’il existe des théories physiques qui utilisent le cadre euclidien, ce qui permet du même coup de travailler la forme et la structure. Tandis qu’il est plus difficile de passer d’une forme fractale conçue par un algorithme à une structure. Par exemple on serait bien en peine s’il fallait réaliser matériellement la ‘fougère’ ci-dessus, car comment faire un objet intègre de plusieurs milliers de points séparés? Tandis que sur un écran, c’est facile puisqu’une image est faite justement de points, des pixels.

Avant que cette géométrie ne soit vraiment utilisable pour l’élaboration de formes architecturales, il y a sans doute un pont à construire pour aider à passer des formes virtuelles issues des algorithmes à des objets matériels. À moins de ne pas se servir d’algorithmes et d’employer plutôt des processus physiques qui construisent directement des objets assimilables à des fractals. Bien que j’imagine difficilement que l’on puisse fabriquer des maisons entières comme ça, dans un proche avenir en tout cas.

En revanche il est tout à fait possible de fabriquer de cette manière des matériaux servant à construire des maisons. Il en existe déjà un, l’aérogel de silice. C’est une sorte de mousse de verre à la transparence bleutée, si légère qu’on dirait de la fumée solidifiée. Bien que peu connu et peu utilisé car encore difficile à produire et cher, ce matériau présente des propriétés remarquables au point de détenir une quinzaine records du monde, dont ceux du meilleur isolant et du solide le plus léger. Il tient du verre la propriété d’être quasi transparent et de l’énorme quantité d’air qu’il contient (99%) d’être à peine plus lourd que l’air (il existe même une préparation obtenue en évacuant une partie de l’air qui permet d’abaisser sa densité à 1 gramme par litre contre 1,2 pour l’air). Il est très isolant thermiquement (certaines préparations atteignent 0,004 W/mK, soit dix fois moins que les isolants traditionnels), étant efficace simultanément pour les trois modes de transmission de la chaleur, la conduction, la convection, le rayonnement. Bien que relativement friable (quoique des additifs permettent maintenant d’y remédier au point de le rendre même flexible) il est très résistant: un petit morceau d’aérogel de deux grammes supporte sans broncher 2,5 kg. Remarque importante: contrairement à ce que son nom pourrait laisser croire il ne s’agit pas d’un gel; il est seulement préparé à partir d’un gel dont est extraite la partie liquide pour être remplacée par de l’air. Il ne s’agit pas non plus de bulles d’air emprisonnées dans du verre. Il s’agit d’une surface siliceuse extrêmement fine, des microparticules de verres sphériques de 2 à 5 nanomètres (un nanomètre vaut un milliardième de mètre ou un millionième de millimètre) fusionnées pour former une structure très poreuse (des pores qui font de l’ordre de 100 nanomètres). On peut sans conteste la qualifier de fractale. Certains aérogels à base de carbone vont jusqu’à 600 mètres carrés par gramme, encore mieux qu’un poumon.

Comprenons bien la démarche: il ne s’agit pas tant d’imiter la Nature que de se servir des représentations que l’on en construit pour stimuler notre imagination. Comme je l’ai déjà souligné, les objets naturels ne sont pas davantage fractals qu’il ne sont euclidiens. La géométrie n’est toujours qu’une abstraction, une création humaine qui fait sens et qui peut stimuler d’autres créations. Certaines comme nos maisons sont vouées à prendre corps dans la matière. C’est là tout le défi de faire la jonction entre la représentation et la réalisation, entre l’esprit et la matière.

S’agissant d’œuvres humaines, tout commence dans l’esprit, tout part donc de l’intention et de la représentation. D’où l’importance de commencer par enrichir voire renouveler notre Vision du monde. Concrètement, et pour rester dans l’architecture, cesser de considérer murs et toits de nos maisons comme des surfaces qui séparent, qui isolent. Commencer à les voir comme des espaces de transition, de filtrage, à un niveau microscopique, de surcroît actifs, c’est-à-dire qui ouvrent plus ou moins le passage en fonction des besoins à diverses substances et énergies comme l’air, l’eau (liquide et vapeur), la lumière, la chaleur, voire les ondes acoustiques. Allant plus loin, cesser de penser en terme de surface mais plutôt à un objet fractal de type surface-volume. Alors nous pourrons concevoir des matériaux qui feront la peau de nos maisons. Des matériaux légers, souples, résistants, durables, recyclables voire autoréparables. Des matériaux respirants, thermorégulants, hygrorégulants, qui rempliront ces fonctions, et d’autres, sans qu’il soit besoin de capteurs ni de dispositifs de régulation électromécaniques faillibles, de par leurs seules propriétés (à l’instar des membranes étanches et respirantes que l’on connaît déjà, comme le Goretex dans l’habillement et le Tyvek dans le bâtiment). On en est encore loin, très loin, mais il est intéressant de savoir que des découvertes vont déjà dans ce sens. On est très loin aussi d’où nous sommes partis, de la représentation naïve de l’espace et de son prolongement dans la géométrie euclidienne. C’est au prix de son dépassement que nous en sommes arrivés à ce point où s’ouvrent des perspectives que l’on n’aurait pu imaginer avant.

sommaire | suite